Question

The circumference of a circle is 136 metures. Find the radius and the area (You need to estimate either 136 metrues to a pefect value or the anser). I will gib branlies

Answer 1

Given :

• Circumference : 136 metres

To find :

• Radius
• Area

Solution :

We know that,

• Circumference = 2πr
• 2πr = 136 m
• r = 136m/2 x π
• r = 21.65m

Hence, our radius would be equal to 21.65m

Also,

we know that,

• Area = πr²
• Area = 1472.54m²

Hence ,our area would be equal to 1472.54m².

Answer 2

The radius of the circle is 22 meters.

The area of the circle is 1472square meters.

Explanation:

Given that the circumference of the circle is 136 meters, we can find the radius using the formula:

`\sf \textsf{Circumference of circle } = 2* \pi * radius`

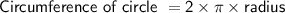
where

• π is equal to 3.141592654

Substituting value in the above formula:

`\sf 136 m = 2 * 3.141592654 * radius`

`\sf 136 m = 6.283185307 * radius`

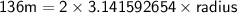
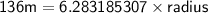
Dividing both sides by 6.283185307.

`\sf (136m)/(6.283185307) = (6.283185307 * radius)/(6.283185307)`

`\sf radius = 21.64507226`

`\sf \sf radius\approx 22 \textsf{ m in perfect value}`

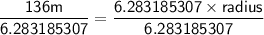
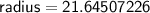
Therefore, the radius of the circle is 22 meters.

Now,

The area of the circle can be found using the formula:

`\sf Area = \pi * radius^2`

where

• π is equal to 3.141592654

Plugging in the radius we found, we get:

`\sf Area = 3.141592654 * (21.64507226 )^2`

`\sf Area = 3.141592654 * 468.5091532`

`\sf Area = 1471.864914 m^2`

`\sf Area = 1472 m^2 \textsf{ in perfect value}`

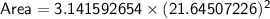
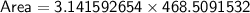
Therefore, the area of the circle is 1472 square meters.