If the sum as well as the product of roots of a quadratic equation is 9, then the equation is: a) x^(2) +9x-18 = 0 b) x^(2) -18x+9=0 c) x^(2) +9x+9=0 d) x^2 -9x +9 = 0 Give a de…

Question

asked Sep 23, 2024 187k views

2 Answers

Mitch Goudy · Answer 1 · 2024-09-23T14:32:48+0000

x_1+x_2=x_1x_2=9

From Vieta's formulas we have

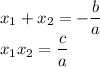
$x_1+x_2=-(b)/(a)\\x_1x_2=(c)/(a)$

Therefore

$-(b)/(a)=9\\(c)/(a)=9\\$

It's not possible to find the exact values of
a,b and
based only on these two equations.

However, if we look at possible answers, we can notice, that in each one
a=1 .

Therefore

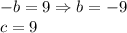
$-b=9\Rightarrow b=-9\\c=9$

Substituting those values into the general quadratic formula, we get

y=x^2-9x+9

Alexandernst · Answer 2 · 2024-09-28T11:12:53+0000

$\implies Question:-$

If the sum as well as the product of roots of a quadratic equation is 9, then the equation is:

a)
x^(2) +9x-18 = 0

b)
x^(2) -18x+9=0

c)
x^(2) +9x+9=0

d)
x^2 -9x +9 = 0

$\implies Answer:-$

d)
x^2 -9x +9 = 0

$\implies Explanation:-$

Given:-

According to the Quadratic formula:-

$\longrightarrow {x}^(2) - ( \alpha + \beta )x + \alpha \beta$

Substituting the values,

$\longrightarrow {x}^(2) - 9x + 9 \\$

So the correct answer is ,

$\longrightarrow {x}^(2) - 9x + 9 \\$

_______________XxAuroraxX<3_______