Question

What's the recursive formula of the geometric sequence below?

2, 6, 18, 54, 162, 486, ...


A. a1 = 2; an = an–1 ∙ (3)^n–1 for n ≥ 1

B. a1 = 2; an = an–1 ∙ (2) for n ≥ 1

C. a1 = 3; an = an–1 ∙ (2^)n–1 for n ≥ 2

D. a1 = 2; an = an–1 ∙ (3) for n ≥ 2

Answer 1

Answer: Choice D

=======================================

Step-by-step explanation

The first term is 2, so we write
`a_1 = 2`. The small subscript "1" is a label to basically say "this is the first term". Then
`a_2` is the next term, and so on.

In general, the nth term is
`a_n` where n is an integer of the set {1,2,3,...}

The term just before the nth term is
`a_(n-1)` it has a subscript of n-1. Whatever n is, subtract off 1. We cannot use n = 1 here. We either write
`n > 1 \text{ or } n \ge 2`

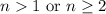
Notice the jump from 2 to 6 is "times 3". We can see that by dividing one term over its previous one

• r = common ratio
• r = term2/term1 = 6/2 = 3
• r = term3/term2 = 18/6 = 3
• r = term4/term3 = 54/18 = 3
• r = term5/term4 = 162/54 = 3
• r = term6/term5 = 486/162 = 3

and so on.

Now because the common ratio is 3, it means we triple each previous term to get the next term.

• 2*3 = 6
• 6*3 = 18
• 18*3 = 54
• 54*3 = 162
• 162*3 = 486

etc.

In general, we triple the (n-1) term
`a_(n-1)` and we must require that
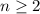`n \ge 2`, or otherwise we'll dip into negative territory.

This gives the recursive rule to be
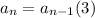`a_n = a_(n-1)(3)` or
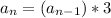`a_n = (a_(n-1))*3`. I like the second format a bit better.

Put another way:

nth term = (previous term)*3

---------------------------

To summarize

`a_1 = 2 = \text{first term}\\\\a_n = (a_(n-1))*3 =\text{recursive rule when } n \ge 2`

This point us to choice D as the final answer.