At 2.85 atm and 225K, the density of hydrogen gas (
 ) is approximately 31.3 g/L using the ideal gas law.
) is approximately 31.3 g/L using the ideal gas law.
To find the density of a gas using the ideal gas law (PV = nRT), you'll need the molar mass of hydrogen (
 ) and the ideal gas constant provided.
) and the ideal gas constant provided.
Given:
Pressure (P) = 2.85 atm
Temperature (T) = 225 K
Gas constant (R) = 0.08206 L atm / (mol K)
Molar mass of hydrogen (
 ) = 2 g/mol
) = 2 g/mol
The ideal gas law equation is PV = nRT. We want to rearrange it to solve for density (d) using the formula:
![\[d = \frac{\text{molar mass} * P}{R * T}\]](https://img.qammunity.org/2024/formulas/chemistry/high-school/101zkl5ij63bzap8o8qbbjt2kcpi6agofc.png)
First, convert the pressure unit to Pa (Pascals) since the ideal gas constant is in the units of L atm/mol K.
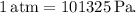
![\[2.85 \, \text{atm} = 2.85 * 101325 \, \text{Pa} = 289103.25 \, \text{Pa}\]](https://img.qammunity.org/2024/formulas/chemistry/high-school/tjmcxnilh2o87932588a2bo34emzwy2b28.png)
Now, plug the values into the formula:
![\[d = \frac{2 \, \text{g/mol} * 289103.25 \, \text{Pa}}{0.08206 \, \text{L atm/mol K} * 225 \, \text{K}}\]](https://img.qammunity.org/2024/formulas/chemistry/high-school/n6q2soymotq1dotv48ggksm5r3ee949zmc.png)
Solving this gives:
![\[d \approx (578206.5)/(18463.5) \approx 31.34 \, \text{g/L}\]](https://img.qammunity.org/2024/formulas/chemistry/high-school/8i0hht64p2012v7twmnew9g17xk99mj2nz.png)
Rounded to three significant figures, the density of the hydrogen gas sample at the given conditions is approximately
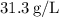 .
.
Question:
What is the density of a sample of hydrogen gas (H2) that exerts 2.85 atm of pressure at 225K?
- Use 0.08206L atmmol K for the ideal gas constant.
- Round the answer to three significant figures.