Question

Can someone just pls no one answering my questions

Answer 1

∠K = 33°

Explanation:

Given angles:

• 
  `\angle K=-2+7x`

• 
  `\angle L=12x-3`

Complementary angles are a pair of angles whose sum is 90°.

In order to find the value of ∠K, we must first find the value of x.

To do this, set the sum of ∠K and ∠L to 90, and solve for x:

`\begin{aligned}\angle K+\angle L&=90^(\circ)\\(-2+7x)^(\circ)+(12x-3)^(\circ)&=90^(\circ)\\-2+7x+12-3&=90\\19x-5&=90\\19x-5+5&=90+5\\19x&=95\\19x/19&=95/19\\x&=5\end{aligned}`

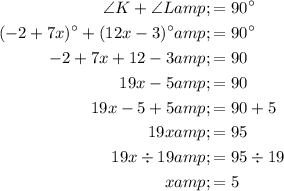
Therefore, the value of x is 5.

Now, substitute the found value of x into the expression for ∠K:

`\begin{aligned}\angle K&=(-2+7(5))^(\circ)\\\angle K&=(-2+35)^(\circ)\\\angle K&=33^(\circ)\end{aligned}`

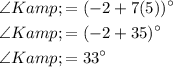
Therefore, the value of ∠K is 33°.

Answer 2

`\sf \angle K =33°\circ`

Explanation:

Given:

`\sf \angle K = -2+7x`

`\sf \angle L = 12x-3`

`\sf \angle K \textsf{ and } \angle L \textsf{ are complementary}`

To find:

[tex,]\sf \angle K =?[/tex]

Solution:

Complementary angles are two angles or more angles whose measures add up to 90°.

So, we have the equation

`\sf \angle K + \angle L = 90^\circ`

Substituting the expressions;

`\sf -2+7x + 12x-3 = 90^\circ`

Combining like terms, we get

`\sf 19x-5= 90^\circ`

Adding 5 to both sides, we get

`\sf 19x = (90+5)^\circ`

`\sf 19x=95^\circ`

Dividing both sides by 19, we get

`\sf x =\left((95)/(19)\right)^\circ`

`\sf x = 5^\circ`

Substituting this value of x.

`\sf \angle K = -2+7(5^\circ) = -2+35^\circ = \boxed{33^\circ }`

`\sf \textsf{Therefore, The value of $\sf \angle K$ is $\sf 33^\circ$ }`