Question

A 7.35 kg block is placed at the top of a frictionless inclined plane angled at 28.3 degrees relative to the horizontal. when released (from rest), the block slides down the full 5.24 meter length of the incline. calculate the speed (magnitude of the velocity) of the block at the bottom of the incline. [start by drawing a free-body diagram for the block.] note that all the information provided may not be necessary to solve the problem.

Answer 1

To calculate the speed of the block at the bottom of the incline, we can use the principles of kinematics and the angle of the incline. The acceleration of the block can be determined using the component of gravity along the incline, and the velocity can be calculated using the equation of motion. The speed of the block at the bottom of the incline is given by
`vf = 9.8 m/s^2 * sin(28.3 degrees) * 5.24 m.`

To solve this problem, we can use the principles of kinematics along the incline. Using the given angle of 28.3 degrees, we can determine the acceleration of the block down the incline using the component of gravity along the incline. The acceleration can be calculated as a = g * sin(θ), where g is the acceleration due to gravity
`(9.8 m/s^2)` and θ is the angle of the incline.

Next, we can use the equation of motion, vf = vi + at, to find the velocity of the block at the bottom of the incline. Since the block starts from rest, the initial velocity is 0. Plugging in the values, we have
`vf = 0 + (9.8 m/s^2 * sin(28.3 degrees) * 5.24 m).`

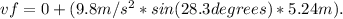
Solving for vf gives us the speed (magnitude of the velocity) of the block at the bottom of the incline.