Answer:
x = 6
Explanation:
Given:
- ST = 1
- SU = 13
- UV = 4+x
- TV = 3x+4
Since SV is a straight line and T and U are the points in SV.
We get:
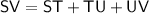

Since the sum of TU and UV equals TV.
Substituting value:
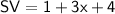
![\sf SV = 3x +5 .......[i]](https://img.qammunity.org/2024/formulas/mathematics/high-school/x2lkspnyj94hg1st9bah9u0unbgepue4b9.png)
Similarly;
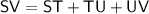
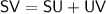
Since the sum of ST and TU equals SU.
Substituting value:
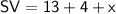
![\sf \sf SV =17+x ......[ii]](https://img.qammunity.org/2024/formulas/mathematics/high-school/gtebmjs0hn1h14j9jg640rjdnqtd8gwuot.png)
Now,
Equating equations [i] and [ii], we get
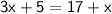
Subtracting both sides by x and 5.
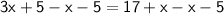
Simplify:
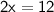
Divide both sides by 2.
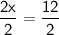
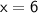
Therefore, the value of x is 6.