Answer:
The least that Pablo can spend on paint is $90.
Explanation:
First, calculate the Area of the Wall Not Covered by the Notice Board:
The area of the wall not covered by the notice board is the same as the area of the square wall minus the area of the notice board.


Now,
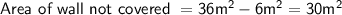
Secondly, Determine the Number of Litres Needed:
Now, we need to determine how many litres of paint are needed to cover 30m^2.
Given that 1 litre of paint covers 2.80m^2, we can calculate the number of litres required:

Since Pablo cannot buy a fraction of a litre, he will need at least 11 litres of paint.
Finally, calculate the Cost:
Pablo can buy either 1-litre cans for $10 each or 2.5-litre cans for $20 each.
Let's check both:
It's expensive in the case of a 2-litre can, so
Let's find the number of cans of 2.5-litre cans costing $20 each if he buys two-and-a-half-litre cans.
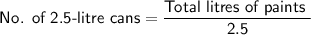
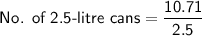
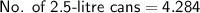
Since Pablo cannot buy a fraction of cans, he will need at least 4 2.5-litre cans and he can buy the remaining paints of 1-litre cans.
The least amount Pablo can spend on paint :
=cost of 4 2.5 litre cans + cost of 1 1-litre can
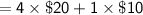
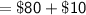
Therefore, the least that Pablo can spend on paint to complete his painting job is $90 if he combines both.