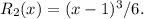Question

Consider the following function. f(x) = x ln(9x), a = 1, n = 2, 0.8 ≤ x ≤ 1.2 a) Approximate f by a Taylor polynomial with degree n at the number a. what is T3(x) and R3(x)?

Answer 1

a) The Taylor polynomial of degree 2 for the function
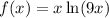`\(f(x) = x \ln(9x)\)` at

(a = 1) is
`\(T_2(x) = (9/2)(x-1) - (9/4)(x-1)^2\)`. The remainder term
`\(R_2(x)\)` is given by
`\(R_2(x) = f''(c)(x-1)^3/3!\)` for some (c) between (1) and (x).

Explanation:

To find the Taylor polynomial
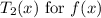`\(T_2(x)\) for \(f(x)\)` at (a = 1), we need the function's values and derivatives at (x = 1). The first derivative
`\(f'(x) = \ln(9x) + 1\)` evaluated at (x = 1) is
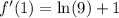`\(f'(1) = \ln(9) + 1\)`. The second derivative
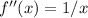`\(f''(x) = 1/x\)` evaluated at (x = 1) is
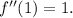`\(f''(1) = 1\).` Now, we can write the Taylor polynomial:

`\[T_2(x) = f(1) + f'(1)(x-1) + (f''(1))/(2!)(x-1)^2.\]`

Substituting
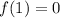`\(f(1) = 0\)` and the derivatives, we get

`\(T_2(x) = (9/2)(x-1) - (9/4)(x-1)^2\)`.

For the remainder term
`\(R_2(x)\)`, we use the Lagrange form of the remainder:

`\[R_2(x) = (f''(c))/(3!)(x-1)^3\]`

for some (c) between (1) and (x). Since
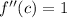`\(f''(c) = 1\)` for any (c),
`\(R_2(x) = (x-1)^3/6\).`