Question

The demand for y is given by y = 256/(p^2). Only two firms produce y. They have identical costs c(y) = y^2. If they agree to collude and maximize their joint profits, how much output will each firm produce?

Answer 1

In a cartel, firms collude to maximize their joint profits. Each firm will produce 8 units of output and charge a price of $4.

Step-by-step explanation:

In a cartel, firms collude to maximize their joint profits. To determine the equilibrium output for each firm, we need to find the quantity that maximizes their joint profits.

In this case, the firms have identical costs, and the demand for the product is given by the equation
`y = 256/(p^2).`

To find the profit-maximizing quantity, we can set the derivative of the total profit function equal to zero and solve for y.

Taking the derivative of the total profit function with respect to y, we get: P(y) = (256/(y^2)) - (y^2). Setting this equal to zero, we find that y = 8.

Substituting this back into the demand equation, we can find the price that the cartel will charge:

`p = \sqrt(256/y) = \sqrt(256/8)`

= 4.

Therefore, each firm will produce 8 units of output and charge a price of $4.

Answer 2

To determine the output each firm will produce when colluding as a cartel, find the point where marginal revenue equals marginal cost by differentiating the total revenue and total cost functions, and solve for the quantity. This quantity, when inserted into the demand curve, will give the price, which can be used to calculate joint profits.

Step-by-step explanation:

When two firms collude to form a cartel, they act as a monopoly to maximize joint profits. To find the cartel's profit-maximizing quantity and price, we first identify the market demand curve y = 256/(
`p^2`), and the cost function c(y) =
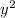`y^2` for each firm. Next, we find the joint profit which is (Price)(Quantity produced) - (Average cost)(Quantity produced). We assume that the firms produce identical quantities. To maximize profits, we need to equate marginal revenue (MR) to marginal cost (MC). Since the firms are colluding, they act as a single producer and hence will find the MR from the total quantity supplied to the market.

To find MR, we need to first find the total revenue function TR, which is P(Q) × Q or 256/Q since P(Q) = 256/
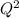`Q^2` and then differentiate this with respect to Q to get MR. To find MC, we differentiate the total cost function, which is c(y) for one firm plus c(y) for the other since they have identical costs, giving us 2y as both are producing the same quantity y. Equating MR = MC allows us to solve for y (quantity produced by each firm) and consequently, P (the price).

Lastly, we can calculate each firm's profit by subtracting the total costs from the total revenue at the found quantities. This involves plugging the quantities into the demand function to find the price at which the total quantity will be sold and then using the cost function to calculate the total cost. The difference is the profit for the cartel, which is split evenly between the two firms.