\bigg(x^2+2x+(1)/(2)\bigg) ^(2x^2+4x)=4

Question

`\bigg(x^2+2x+(1)/(2)\bigg) ^(2x^2+4x)=4`

Answer 1

x ≈ -2.498, -1.802, -0.198, 0.498 (irrational solutions)

x = -1 (rational solution)

Explanation:

You want the solutions to (x² +2x +1/2)^(2x² +4x) = 4.

Rewrite

Using z = (x +1)², we can rewrite the equation to ...

`\left(z -(1)/(2)\right)^(2(z-1))=4\\\\\\\left(z-(1)/(2)\right)^(z-1)=\pm2\qquad\text{take square root}`

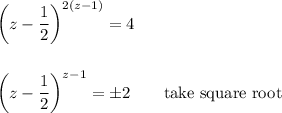
Once a value of z is found, the corresponding x value is ...

x = -1 ± √z

Solution space

In general, such a combination of polynomial and exponential functions has no solution by algebraic methods. A graphing calculator can be very helpful for real solutions. Otherwise, it is a "guess and check" process.

For z < 1/2, we have a negative number to a negative power. This has real values only if the negative power is rational with an even numerator or an odd denominator. We notice that for z = 0, this evaluates to ...

(-1/2)^(-1) = -2 . . . . . a solution to the equation

For this value of z, ...

0 = (x +1)² ⇒ x = -1

For z > 1/2, there are two real solutions. The attached graph shows these.

• z = 0.643267266867 ⇒ x = -1 ± 0.802039442214
• z = 2.24499036289 ⇒ x = -1 ± 1.49832919043

__

Additional comment

More significant figures are found using Newton's method iteration, starting with the value indicated on the graph.

Most graphing calculators have trouble graphing exponential functions with a negative base. The graph is a discontinuous set of points that have positive and negative values. Some calculators simply treat the function as undefined for exponents that are not integers.

<95141404393>