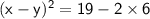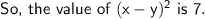If (x + y)^2 = 31 and xy=6, what is the value of (x-y)^2

Question

asked Mar 16, 2024 206k views

1 Answer

Ponml · Answer 1 · 2024-03-23T10:18:57+0000

Answer:

Value of (x-y)^2 is 7.

Explanation:

Given:

Using the following identity:

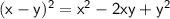
$\sf (x - y)^2 = x^2 - 2xy + y^2$

Let's use this information to calculate:

$\sf (x - y)^2$

Expand:
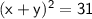
$\sf (x + y)^2 = 31$

$\sf x^2 + 2xy + y^2 = 31$

Substitute the value of xy.

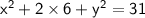
$\sf x^2 + 2* 6 + y^2 = 31$

Subtract 12 from both sides:

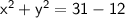
$\sf x^2 + y^2 = 31 - 12$

$\sf x^2 + y^2 = 19$

Now, we have x^2 + y^2.

To find (x - y)^2, using the identity:

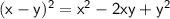
$\sf (x - y)^2 = x^2 - 2xy + y^2$

Substitute the values:

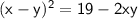
$\sf (x - y)^2 = 19 - 2xy$

Substitute the value of xy:

$\sf (x - y)^2 = 19 - 2 * 6$

$\sf (x - y)^2 = 19 - 12$

$\sf (x - y)^2 = 7$

$\textsf{ So, the value of }\sf (x - y)^2\textsf{ is } 7.$