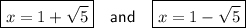Question

Use the quadratic formula to determine the exact solutions to the equation. xsquared2−2x−4=0 Enter your answers in the boxes.

Answer 1

`x=1+√(5)`

`x=1-√(5)`

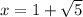
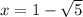
Explanation:

The quadratic formula is a mathematical equation used to find the solutions (roots) of a quadratic equation of the form ax² + bx + c = 0, where a, b, and c are constants and "x" represents the unknown variable.

`\boxed{\begin{array}{c}\underline{\sf Quadratic\;Formula}\\\\x=(-b \pm √(b^2-4ac))/(2a)\quad\textsf{when}\; ax^2+bx+c=0 \\\\\end{array}}`

Given quadratic equation:

`x^2-2x-4=0`

Therefore, the values of a, b and c are:

• a = 1
• b = -2
• c = -4

To use the quadratic formula to determine the exact solutions of the given equation, substitute the values of a, b and c into the quadratic formula and solve for x:

`x=(-(-2) \pm √((-2)^2-4(1)(-4)))/(2(1))`

`x=(2 \pm √(4+16))/(2)`

`x=(2 \pm √(20))/(2)`

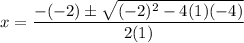
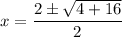
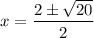
Rewrite 20 as 2² · 5:

`x=(2 \pm √(2^2\cdot 5))/(2)`

`\textsf{Apply the radical rule:} \quad √(ab)=\sqrt{\vphantom{b}a}√(b)`

`x=(2 \pm √(2^2)√(5))/(2)`

`\textsf{Apply the radical rule:} \quad √(a^2)=a, \quad a \geq 0`

`x=(2 \pm 2√(5))/(2)`

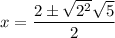
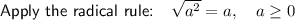
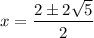
Simplify by factoring out the common term 2:

`x=1 \pm √(5)`

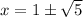
Therefore, the exact solutions of the given quadratic equation are:

`\boxed{x=1+√(5)}\quad\textsf{and}\quad\boxed{x=1-√(5)}`

Answer 2

`\sf x =1+ √(5) \approx 3.236`

`\sf x =1- √(5) \approx -1.236`

Explanation:

Using the quadratic formula to determine the exact solutions to the equation x² − 2x − 4 = 0.

The quadratic formula is:

`\sf x = ( -b \pm √(b^2 - 4ac))/( 2a)`

where a = 1, b = -2, and c = -4.

Plugging these values into the formula, we get:

`\sf x = (2 \pm √((-2)^2 - 4 * 1 * -4))/(2* 1)`

`\sf x = (2 \pm √(20))/(2)`

`\sf x = (2 \pm 2√(5))/(2)`

Taking common 2.

`\sf x = 2(1 \pm 1 √(5))/(2)`

Reducing value of fraction

`\sf x =1\pm √(5)`

Therefore, the solutions to the equation are:

When positive:

`\sf x =1+ √(5) \approx 3.236`

When negative:

`\sf x =1- √(5) \approx -1.236`

Therefore, value of x is:

`\sf x =1+ √(5) \approx 3.236`

`\sf x =1- √(5) \approx -1.236`