Question

Solve and check for extraneous solutions please :)

Answer 1

There are no extraneous solutions.

7 and -9 are the valid solutions

Explanation:

Given:

• 3-10|k+1| =-78

To find :

• Value of k.

Solution:

Isolate the absolute value.

`\sf -10|k+1| = -78 - 2`

`\sf -10|k+1| = -80`

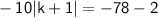
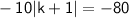
Divide both sides by -10.

`\sf |k+1| = (-80)/(10)`

`\sf |k+1| = 8`

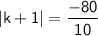
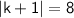
The absolute value of an expression is its distance from zero.

It has two solutions, one negative and one positive.

The negative solution is:

`\sf k+1 = -8`

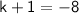
Solving for k, we get:

`\sf k = -8-1`

`\sf k = -9`

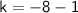
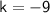
The positive solution is:

`\sf k+1 = 8`

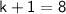
Solving for k, we get:

`\sf k = 8-1`

`\sf k = 7`

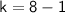
We need to check both solutions to make sure they are not extraneous.

An extraneous solution is a solution that makes the original equation undefined.

Now that we have two potential solutions, k = 7 and k = -9, let's check them in the original equation to see if they are extraneous:

For k = 7:

`\sf 2 - 10|7 + 1| = -78`

`\sf 2 - 10|8| = -78`

`\sf 2 - 80 = -78`

`\sf -78 = -78 (True)`

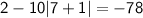
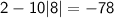
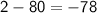
For k = -9:

`\sf 2 - 10|-9 + 1| = -78`

`\sf 2 - 10|-8| = -78`

`\sf 2 - 10*8 = -78`

`\sf 2 - 80 = -78`

`\sf -78 = -78 (True)`

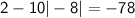
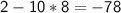
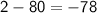
Both solutions, k = 7 and k = -9, satisfy the original equation, so there are no extraneous solutions.

7 and -9 are the valid solutions to the equation.