Question

The midpoint of CD is M=(2, 5). One endpoint is C = (−1, 2). Find the coordinates of the other endpoint, D. D (?, ?) M (2, 5) C (-1, 2)​

Answer 1

D = (5, 8)

Explanation:

To find the coordinates of the endpoint D, given the midpoint M and one endpoint C, use the midpoint formula.

`\boxed{\begin{minipage}{7.4 cm}\underline{Midpoint formula}\\\\$M(x,y)=\left((x_2+x_1)/(2),(y_2+y_1)/(2)\right)$\\\\\\where $(x_1,y_1)$ and $(x_2,y_2)$ are the endpoints.\\\end{minipage}}`

Given:

• M = (2, 5)
• C = (-1, 2)

Substitute the values into the formula:

`(x_M,y_M)=\left((x_D+x_C)/(2),(y_D+y_C)/(2)\right)`

`(2,5)=\left((x_D-1)/(2),(y_D+2)/(2)\right)`

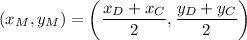
Solve for the x-coordinate:

`\begin{aligned}(x_D-1)/(2)&=2\\\\(x_D-1)/(2)\cdot2&=2\cdot2\\\\x_D-1&=4\\\\x_D-1+1&=4+1\\\\x_D&=5\end{aligned}`

Solve for the y-coordinate:

`\begin{aligned}(y_D+2)/(2)&=5\\\\(y_D+2)/(2)\cdot2&=5\cdot2\\\\y_D+2&=10\\\\y_D+2-2&=10-2\\\\y_D&=8\end{aligned}`

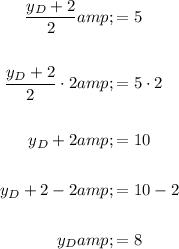
Therefore, the coordinates of endpoint D are (5, 8).