Question

A photon of yellow light has a wavelength of 579 nm. Calculate the energy of that photon (J) and enter your answer in exponential format (example 1.23E4) with two decimal places and no units.

Answer 1

Approximately
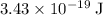`3.43 * 10^(-19)\; {\rm J}` assuming that the wavelength was measured in vacuum.

Step-by-step explanation:

Given the wavelength, the energy of this photon can be found in the following steps:

• Find the frequency
  `f`of this photon from wave speed
  `v` and wavelength
  `\lambda` using the equation
  `f = v / \lambda`.
• Find the energy of the photon from its frequency using the equation
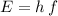  `E = h\, f`, where
  `h` is Planck's Constant.

Apply unit conversation and ensure that wavelength is measured in standard units:

`\begin{aligned} \lambda &= 579\; {\rm nm} \\ &= (579\; {\rm nm}) * \frac{1\; {\rm m}}{10^(9)\; {\rm nm}} \\ &= 5.79 * 10^(-7)\; {\rm m} \end{aligned}`.

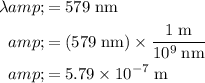The speed of electromagnetic waves is the same as the speed of light. Assume that the wavelength of this photon was measured in vacuum, where the speed of light in vacuum is
`c \approx 3.00 * 10^(8)\; {\rm m\cdot s^(-1)}`. Given that wavelength is
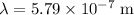`\lambda = 5.79 * 10^(-7)\; {\rm m}`, the frequency of this photon would be:

`\begin{aligned}f &= (v)/(\lambda) \\ &\approx \frac{3.00 * 10^(8)\; {\rm m\cdot s^(-1)}}{5.79 * 10^(-7)\; {\rm m}} \\ &\approx 5.1813 * 10^(14)\; {\rm s^(-1)}\end{aligned}`.

Look up the value of Planck's Constant:
`h \approx 6.6261 * 10^(-34)\; {\rm J \cdot s}`. Apply the equation
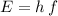`E = h\, f` to find the energy of this photon from its frequency:

`\begin{aligned}E &= h\, f \\ &\approx (6.6261 * 10^(-34)\; {\rm J\cdot s})\, (5.1813 * 10^(14)\; {\rm s^(-1)}) \\ &\approx 3.43 * 10^(-19)\; {\rm J}\end{aligned}`.

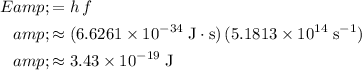In other words, the energy of this photon would be approximately
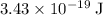`3.43 * 10^(-19)\; {\rm J}`.