Question

X^logx=10000

Find x.

Answer 1

x = {100, 1/100}

Explanation:

To find the value of 'x' in the the given equation, we'll use a combination of logarithmic and exponential properties to isolate 'x'.

Given equation:

`x^(\log(x))=10000`

`\hrulefill`

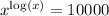
First, we take the natural logarithm on both sides of the equation:

`\Longrightarrow \ln(x^(\log(x)))=\ln(10000)`

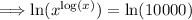
We know 10000 = 10⁴, substitute this in:

`\Longrightarrow \ln(x^(\log(x)))=\ln(10^4)`

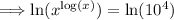
Using the properties of logarithms, we can move the exponent in the argument out front:

`\Longrightarrow \log(x)\ln(x)=4\ln(10)`

Looking at the left-hand side of the equation, we can apply the change of base property:

`\boxed{\left\begin{array}{ccc}\text{\underline{Change of Base:}}\\\\\log_a(b)=(\log_c(b))/(\log_c(a))\\\\\text{Where $c$ is the new base} \end{array}\right}`

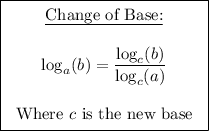
`\Longrightarrow \log(x)\log_e(x)=4\ln(10) \ \Big[\because \ln(x) = \log_e(x)\Big]\\\\\\\\\Longrightarrow \log(x)\Big((\log(x))/(\log(e)) \Big)=4\ln(10) \\\\\\\\\Longrightarrow (\log(x)^2)/(\log(e))=4\ln(10)`

If we let log(x) = u, we can make a substitution:

`\Longrightarrow (u^2)/(\log(e))=4\ln(10)`

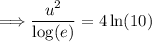
Solving for 'u', we get:

`\Longrightarrow u^2=\log(e)\cdot4\ln(10)\\\\\\\\\Longrightarrow u^2=4\\\\\\\\\therefore u = \pm 2`

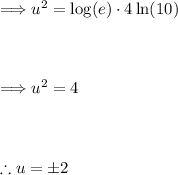
Now we can solve for both values of 'x'. Substitute back in u = log(x) :

When u = 2:

`\Longrightarrow \log(x) = 2\\\\\\\\\Longrightarrow x = 10^2 \ \Big[\because \text{if $\log_a(b) = c$ then $b = a^c$} \Big] \\\\\\\\\therefore \boxed{x = 100}`

When u = -2:

`\Longrightarrow \log(x) = -2\\\\\\\\\Longrightarrow x = 10^(-2) \ \Big[\because \text{if $\log_a(b) = c$ then $b = a^c$} \Big]\\\\\\\\ \Longrightarrow x = (1)/(10^2) \\\\\\\\\therefore \boxed{x = (1)/(100) }`

Thus, the problem is solved.