Question

( please help)

1.1) Determine the number of pillars around the perimeter of the temple

1.2) If the diameter of each pillar is 60cm, and the height of the pillar is 10m. Work only in centimeters.

1.2.1) Calculate the surface area of a singular pillar where only the top is included.

1.2.2) Use your answer from 1.2.1) to calculate the total surface area of 36 pillars. Round you answer off to 1 decimal place.

Answer 1

1.1) There are 36 pillars around the perimeter of the temple.

1.2) Volume (one pillar) = 900,000π cm³ ≈ 2,827,433.4 cm³ (1 d.p.)

Surface Area (one pillar) = 61,800π cm² ≈ 194,150.4 cm² (1 d.p.)

1.2.1) 60,900π cm² ≈ 191,323.0 cm² (1 d.p.)

1.2.2) 6,887,627.7 cm² (1 d.p.)

Explanation:

Part 1.1

The Doric Temple known as "Hera II" is an ancient Greek temple located in Paestum, Italy. This temple is one of the best-preserved ancient Greek temples and is dedicated to the goddess Hera.

It has 6 pillars along each shorter side, and 14 pillars along each longer side. Therefore, there are 36 pillars in total around the perimeter of the temple.

`\hrulefill`

Part 1.2

The diameter of each pillar is 60 cm.

The height of each pillar is 10 m.

As we need to work only in centimeters, we first need to convert the height of each pillar into centimeters by multiplying the number of meters by 100 (as 1 m = 100 cm). Therefore, the height of each pillar in centimeters is:

h = 10 × 100 = 1,000 cm

The pillars are cylindrically-shaped. Therefore, to find their volume and surface area, we can model them as cylinders.

The diameter of a circle is twice its radius.

Therefore, as the diameter of each pillar is 60 cm, its radius (r) is 30 cm.

Volume

The formula for the volume of a cylinder with radius r and height h is:

`V=\pi r^2 h`

To calculate the volume of each pillar, substitute r = 30 and h = 1000 into the formula:

`V=\pi \cdot 30^2 \cdot 1000`

`V=\pi \cdot 900 \cdot 1000`

`V=900000\pi`

`V= 2827433.38823...`

`V=2827433.4\; \sf cm^3\;\sf (1\;d.p.)`

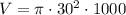
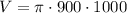
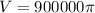
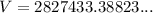
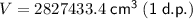
Therefore, the volume of each pillar is exactly 900,000π cm³, or approximately 2,827,433.4 cm³ (rounded to one decimal place).

Surface Area

The formula for the surface area of a cylinder with radius r and height h is:

`S.A.=2\pi r^2+2\pi rh`

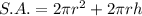
To calculate the surface area of each pillar, substitute r = 30 and h = 1000 into the formula:

`S.A.=2\pi \cdot 30^2+2\pi\cdot30\cdot1000`

`S.A.=2\pi \cdot 900+2\pi\cdot30000`

`S.A.=1800\pi +60000\pi`

`S.A.=61800\pi`

`S.A.=194150.4259918...`

`S.A.=194150.4\; \sf cm^2\;(1\;d.p.)`

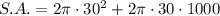
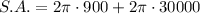
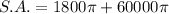
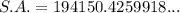
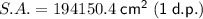
Therefore, the surface area of each pillar is exactly 61,800π cm², or approximately 194,150.4 cm² rounded to one decimal place.

`\hrulefill`

Part 1.2.1

The surface area of a singular pillar where only the top is included is the area of one circular base and the lateral surface area of the cylinder. Therefore, the formula for this is:

`S.A.=\pi r^2+2\pi rh`

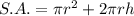
Substitute r = 30 and h = 1000 into the formula:

`S.A.=\pi \cdot 30^2+2\pi\cdot30\cdot1000`

`S.A.=\pi \cdot 900+2\pi\cdot30000`

`S.A.=900\pi +60000\pi`

`S.A.=60900\pi`

`S.A.=191322.9926...`

`S.A.=191323.0\; \sf cm^2\;(1\;d.p.)`

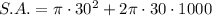
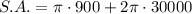
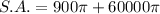
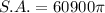
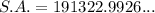
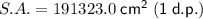
Therefore, the surface area of each pillar where only the top is included is exactly 60,900π cm², or approximately 191,323.0 cm² rounded to one decimal place.

`\hrulefill`

Part 1.2.2

Using the exact surface area from part 1.2.1 of 60,900π cm², we can calculate the total surface area of all 36 pillars by multiplying the surface area of one pillar by 36:

`\textsf{Total}\;S.A.=60900\pi \cdot 36`

`\textsf{Total}\;S.A.=2192400\pi`

`\textsf{Total}\;S.A.=6887627.73373...`

`\textsf{Total}\;S.A.=6887627.7\; \sf cm^2\;(1\;d.p.)`

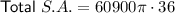
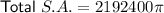
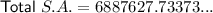
Therefore, the total surface area of all 36 pillars is 6,887,627.7 cm² (rounded to one decimal place).