Question

Simplify (6a+b)(a+b)-7b(a+b) all over 2a²-2b²

Answer 1

3

Explanation:

((6a+b)(a+b)-7b(a+b))/(2a² - 2b²) =

(6a² + 6ab + ab + b² - 7ab - 7b²)/(2a²- 2b²) =

(6a² - 6b²)/(2a²-2b²) =

(3(2a² - 2b²))/(2a² - 2b²) =

3/1 =

3.

Answer 2

`\huge{\boxed{3}}`

Explanation:

We can simplify the expression:

`((6a+b)(a+b)-7b(a+b))/(2a^2-2b^2)`

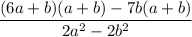
by...

1. expanding and combining like terms in the numerator
2. factoring the numerator and denominator
3. canceling like terms in the numerator and denominator

First, we can expand the numerator using the distributive property, which states that:

`a(b + c) = ab + ac`

This can also be complicated to:

`(a + b)(c + d) = ac + ad + bc + bd`

↓ applying this to the expression at hand

`(6a(a) + 6a(b) + b(a) + b(b) - 7b(a) - 7b(b))/(2a^2-2b^2)`

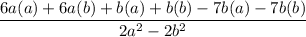
↓ simplifying the numerator

`(6a^2 + 6ab + ab + b^2 - 7ab - 7b^2)/(2a^2-2b^2)`

Next, we can group, then combine like terms in the numerator.

↓ grouping like terms

`(6a^2 + (6ab + ab - 7ab) + (b^2 - 7b^2))/(2a^2-2b^2)`

↓ simplifying the values within the parentheses

`(6a^2 - 6b^2)/(2a^2-2b^2)`

Finally, we can factor the numerator and denominator, then cancel the like factor(s).

`(6(a^2 - b^2))/(2(a^2 - b^2))`

↓ canceling the like factor
`(a^2 - b^2)`

`(6)/(2)`

↓ executing the division

`\huge\boxed{3}`