Question

Calculate the sum of all the odd numbers less than 300

Answer 1

Explanation:

The smallest odd number is 1 and the largest odd number less than 300 is 299. So the first and last term of the sequence is 1 and 299. Two consecutive odd numbers have a difference of 2. The sequence is 1,3,5,7.....299.

We have to find the sum of all the odd numbers less than 300 or sum of all terms of this sequence,

Finding no. of terms:

`\boxed{a_n = a + (n-1)d}`

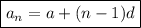
Where a_n is the last term or nth term, d is the difference and a is the first term. Substituting values to find the value of n,

`\hookrightarrow \: 299 = 1 + (n - 1)2`

`\hookrightarrow \: 298 = 2(n - 1)`

`\hookrightarrow \: n - 1 = 149`

`\hookrightarrow \: n = 150`

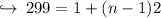
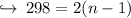
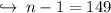
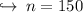
Sum of all odd number than 300:

`\boxed{Sn = (n)/(2) [2a + (n-1)d]}`

where S_n is sum of all terms. Putting the required values to find the sum of all odd terms < 300,

`\hookrightarrow \: Sn = (150)/(2) (2 * 1 + (150 - 1)2)`

`\hookrightarrow \: Sn  = 75(2 + 298)`

`\hookrightarrow \: Sn  = 75 * 300`

`\hookrightarrow \: Sn  = \boxed{22500}`

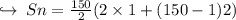
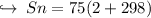
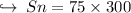
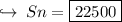
`\therefore` Sum of all odd terms less than 300 is 22500