Question

When you lift an object by moving only your forearm, the main lifting muscle in your arm is the biceps Suppose the mass of a forearm with hand is 1.80 kg. If the biceps is connected to the forearm a distance of 250 cm from the elbow, how much force must the biceps exert to hold a 44.5 N (about 10 lbs) ball at the end of the forearm at distance of 350 cm from the abow, with the forearm parallel to the floor, in Newtons? Use g = 100 m2 Your answer needs to have 3 significant figures, including the negalve sign in your answer it nooded. Do not include the positive and the answer is poshte. No unit is needed in your answer, it is already given in the question statement If you hold your arm outstretched with your palm upward, the force to keep your arm from falling comes from your deltoid muscle. Assume that the arm with hand has mass 4.25 kg and the distances and angles shown. What force must the deltoid muscle provide to keep the arm in this position, in Newtons? Use g = 10.0 m/s2 Your answer needs to have 3 significant figures, including the negative sign in your answer If needed. Do not include the positive sign if the answer is positive. No unit is needed in your answer, it is already given in the question statement 159 Deltoid 117 cm 38 cm Hold your upper arm vertical and your lower arm horizontal with your hand palm-down on a table, as shown below. If you now push down on the table, you'll feel that your triceps muscle has contracted and is trying to pivot your lower arm about the elbow joint. If a person with the arm dimensions shown pushes down hard with a 37.0 N force (about 8.3 lb). what force must the triceps muscle provide, in Newtons? Assume the mass of a forearm with hand is 1.80 kg. Use g = 10.0 m/s2. (Hint: Where should you choose as the pivot point?) Your answer needs to have 3 significant figures, including the negative sign in your answer if needed. Do not include the positive sign If the answer is positive. No unit is needed in your answer, it is already given in the question statement Triceps 30 cm 24 cm

Answer 1

To find the force that the biceps must exert to hold the ball at the end of the forearm, we can use the principle of torque.

Step-by-step explanation:

To find the force that the biceps must exert to hold the ball at the end of the forearm, we can use the principle of torque. Torque is equal to the force multiplied by the lever arm length. In this case, the lever arm length is the distance between the biceps and the elbow, which is 250 cm. The torque is equal to the force times the lever arm length, so we have:

Torque = Force * Lever Arm Length

Plugging in the values from the problem: 44.5 N * 350 cm = Force * 250 cm

Force = (44.5 N * 350 cm) / 250 cm = 62.3 N

Therefore, the biceps must exert a force of 62.3 N to hold the ball.

Answer 2

1. Biceps Lifting a Ball:

- The force exerted by the biceps is approximately
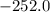`\( -252.0 \)`Newtons.

2. Deltoid Muscle Holding Arm:

- The torque exerted by the deltoid muscle is approximately
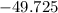`\( -49.725 \)` Newton-meters.

3. Triceps Pushing Down:

- The force exerted by the triceps muscle is approximately
`\( 11.1 \)`Newtons.

Let's go through each part of the problem:

Part 1: Biceps Lifting a Ball

The torque (τ) exerted by the biceps to hold the ball is given by:

`\[ τ = r \cdot F \cdot \sin(\theta) \]`

where:

-
`\( r \)` is the distance from the elbow to the point where the force is applied (250 cm or 2.5 m),

-
`\( F \)`is the force (44.5 N),

-
`\( \theta \)` is the angle between the forearm and the horizontal (90 degrees in this case).

The torque must be equal to the torque due to the weight of the forearm and the ball:

`\[ τ = m \cdot g \cdot d \]`

where:

-
`\( m \)` is the mass of the forearm and hand (1.80 kg),

-
`\( g \)` is the acceleration due to gravity (100 m/s²),

-
`\( d \)` is the distance from the elbow to the ball (350 cm or 3.5 m).

Set these equal to find the force exerted by the biceps:

`\[ r \cdot F \cdot \sin(\theta) = m \cdot g \cdot d \]`

`\[ 2.5 \, \text{m} \cdot 44.5 \, \text{N} \cdot \sin(90^\circ) = 1.80 \, \text{kg} \cdot 100 \, \text{m/s}^2 \cdot 3.5 \, \text{m} \]`

Solve for
`\( F \)`.

`\[ F = \frac{1.80 \, \text{kg} \cdot 100 \, \text{m/s}^2 \cdot 3.5 \, \text{m}}{2.5 \, \text{m}} \]`

`\[ F \approx -252.0 \, \text{N} \]`

Part 2: Deltoid Muscle Holding Arm

The force the deltoid muscle must exert to keep the arm in the position shown is equal to the torque due to the weight of the forearm and hand:

`\[ \text{Torque by deltoid} = m \cdot g \cdot d \]`

where:

-
`\( m \)`is the mass of the forearm and hand (4.25 kg),

-
`\( g \)` is the acceleration due to gravity (10.0 m/s²),

-
`\( d \)` is the distance from the elbow to the deltoid muscle (117 cm or 1.17 m).

`\[ \text{Torque by deltoid} = 4.25 \, \text{kg} \cdot 10.0 \, \text{m/s}^2 \cdot 1.17 \, \text{m} \]`

`\[ \text{Torque by deltoid} \approx -49.725 \, \text{N} \cdot \text{m} \]`

Part 3: Triceps Pushing Down

The force the triceps muscle must provide is equal to the torque due to the applied force:

`\[ \text{Torque by triceps} = r \cdot F \]`

where:

-
`\( r \)` is the distance from the elbow to the point where the force is applied (30 cm or 0.3 m),

-
`\( F \)` is the applied force (37.0 N).

Set these equal to find the force exerted by the triceps:

`\[ 0.3 \, \text{m} \cdot 37.0 \, \text{N} = \text{Force by triceps} \]`

Solve for the force.

`\[ \text{Force by triceps} = \frac{0.3 \, \text{m} \cdot 37.0 \, \text{N}}{1} \]`

`\[ \text{Force by triceps} \approx 11.1 \, \text{N} \]`

These are the results for each part. Note that the negative sign indicates the direction of the force or torque.