Question

Find the mean, median, mode, range, and outliers:

10.4, 13.9, 12.3, 14.2, 5.7, 10.4, 15.3, 10.5, 13.9

Answer 1

• Mean = 11.9
• Median = 12.3
• Mode = 10.4 and 13.9
• Range = 9.6
• Outliers = None

Explanation:

To find the mean, median, mode, range, and outliers for the given data set:

10.4, 13.9, 12.3, 14.2, 5.7, 10.4, 15.3, 10.5, 13.9

Let's start by arranging the data in ascending order:

5.7, 10.4, 10.4, 10.5, 12.3, 13.9, 13.9, 14.2, 15.3

Mean (Average):

The mean is calculated by summing up all the values and dividing by the total number of values.

`\begin{aligned} &\sf Mean =( (5.7 + 10.4 + 10.4 + 10.5 + 12.3 + 13.9 + 13.9 + 14.2 + 15.3) )/(9) \\\\&\sf Mean = (106.6)/(9)\\\\&\sf Mean =11.844\end{aligned}`

`\hrulefill`

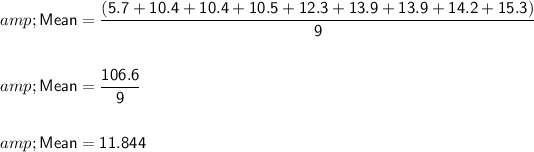
Median:

The median is the middle value of a data set when arranged in ascending order.

Since there are 9 data points, the middle value is the 5th value, which is 12.3.

`\hrulefill`

Mode:

The mode is the value that appears most frequently in the data set.

In this case, both 10.4 and 13.9 appear twice, making them the modes.

`\hrulefill`

Range:

The range is the difference between the maximum and minimum values in the data set.

`\sf Range = 15.3 - 5.7 = 9.6`

`\hrulefill`

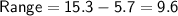
Outliers:

Outliers are values that are significantly higher or lower than the rest of the data points. To identify outliers, you can use the interquartile range (IQR) method. First, calculate the IQR:

Arrange data: 5.7, 10.4, 10.4, 10.5, 12.3, 13.9, 13.9, 14.2, 15.3

First Quartile (Q1):

`\textsf{ The median of the lower half }\sf = (10.4+ 10.4)/(2) = 10.4`

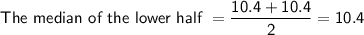
(average of the two middle values)

Third Quartile (Q3):

`\textsf{The median of the upper half =}\sf (13.9+ 14.2)/(2)= 14.05`

(average of the two middle values)

IQR
`\sf IQR = Q3 - Q1 = 14.05-10.4 = 3.65`

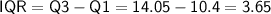
Now, calculate the lower and upper bounds for outliers:

`\sf \textsf{ Lower Bound }: Q1 - 1.5 * IQR = 10.4 - 1.5 * 3.65 =4.925`

`\sf \textsf{ Upper Bound: }Q3 + 1.5 * IQR = 14.05 + 1.5 * 3.65 = 19.525`

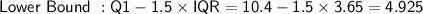
None of the data points fall outside the lower and upper bounds, so there are no outliers in this data set.

`\hrulefill`

To summarize:

• Mean = 11.9
• Median = 12.3
• Mode = 10.4 and 13.9
• Range = 9.6
• Outliers = None