Question

(a) Find the 2nd term of a geometric sequence whose first and third terms are 2/3 and 3/2 and respectively.​

Answer 1

The second term of the geometric sequence is 1.

Explanation:

The nth term of a geometric sequence is given by the formula:

`\sf a_n = a_1 r^((n - 1))`

`\textsf{ where $\sf a_n $ is the nth term, $\sf a_1 $is the first term, and r is the common ratio.}`

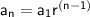
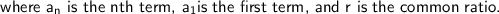
In this case, we are given that:

`\sf a_1 = (2)/(3) \textsf{ and }a_3 = (3)/(2)`

Let's substitute these values of the third term and 1st term into the formula to find the common ratio r:

`\sf (3)/(2) = (2)/(3)r^((3-1))`

`\sf \textsf{ \underline{Multiplying }both side by :}(3)/(2)`

`\sf \sf (3)/(2) * (3)/(2) = (2)/(3)r^((3-1))* (3)/(2)`

`\sf (9)/(4) = r^2`

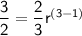
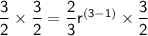
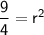
Taking square root on both sides:

`\sqrt{\sf (9)/(4) }= \sf √( r^2)`

`\sf r =(3)/(2)`

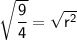
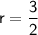
Now that we know the common ratio, we can find the second term by substituting the value of the common ratio and 1st term into the formula:

`\sf a_2 =(2)/(3)* \left((3)/(2)\right)^((2-1))`

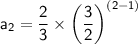
Solve power

`\sf a_2 =(2)/(3)* \left((3)/(2)\right)`

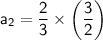
Simplify

`\sf a_2 = 1`

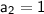
Therefore, the second term of the geometric sequenceS