Question

Help with 5 and six please for brianliest 100 points

Answer 1

5. 42°
6. 128°

Explanation:

Question 5)
The description in this box says that the dashed line is vertical and the ground is horizontal. This means when they intersect, the angle they create will be a right angle which always has a measurement of 90 degrees, or 90°. With this information, we can determine that the sum (adding them together) of any angles between the dashed line and the horizontal line be equal to 90°. These angles are called complementary angles, and they resemble the work you've done for question 3. So now we can set up an equation to solve for x.

x + 48 = 90
x + 48 - 48 = 90 - 48
x + 0 = 42
x = 42

The unknown angle is 42 degrees, or 42°.

Question 6)
In viewing the Great Pyramid of Giza from the side, both the object or animal in this box and the pyramid itself are on the same plane. However, the angles created by either side of the wall will be different. Because they share the same plane but are separated by an intersecting line (AKA the wall of the pyramid creating their angles), these angles are called supplementary angles and their sum will be equal to 180°. This is much like what you did for questions 1 and 2. With this information, we can set up an equation and once again solve for x.

x + 52 = 180
x + 52 - 52 = 180 - 52
x + 0 = 128
x = 128

The value of x is 128 degrees, or 128°.

Answer 2

Question no. 5: x = 42°

Question no. 5: x = 128°

Explanation:

For Question 5.

Since the dashed line is vertical, it is perpendicular to the ground. The angle between the kite string and the dashed line is 48°.

This makes the angle between the kite string and the ground (which includes the unknown angle x) its complementary angle.

Complementary angles add up to 90°.

Therefore, the relationship between the given 48° angle and the unknown angle x can be expressed as:

`\sf 48^\circ + x = 90^\circ`

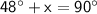
Subtract 48° from both sides of the equation:

`\sf x = 90^\circ - 48^\circ`

`\sf x = 42^\circ`

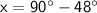
So, the value of x is 42°.

`\hrulefill`

For Question 6.

A linear pair consists of two adjacent angles whose non-common sides form a straight line.

In a linear pair, the sum of the angles is always 180°.

In the case of the Great Pyramid side view problem, if the sides of the pyramid make an angle of 52° with respect to the ground, then the angle between the sides and the ground is 52°.

This angle is one part of a linear pair. The other angle in the linear pair is x, which is the angle formed between the sides and the base of the pyramid.

Since the angles in a linear pair add up to 180°, we have

`\sf 52^\circ + x = 180^\circ`

Subtract 52° from both sides of the equation:

`\sf x = 180^\circ - 52^\circ`

`\sf x = 128^\circ`

So, the value of angle x is 128°.