Question

Determine the radius of the circular orbit of the asteroid, if the angular velocity of its revolution around the Sun is ω, and the mass of the Sun is M

Answer 1

`\displaystyle \sqrt[3]{(G\, M)/(\omega^(2))}`,

Or equivalently:

`\displaystyle \left((G\, M)/(\omega^(2))\right)^(1/3)`.

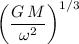(Note the cube root.)

Step-by-step explanation:

The radius of the orbit of this asteroid can be found in the following steps:

• Derive an expression for the net force on the asteroid from the fact that it is in a centripetal motion.
• Derive the magnitude of gravitational attraction between the Sun and this asteroid. Assuming that there are no other force on this asteroid, obtain an alternative expression for the net force on this asteroid.
• Equate the two expressions from the net force on this asteroid and solve for the radius of the orbit.

The asteroid in this question is moving in a circular orbit, meaning that it is in a centripetal motion. The acceleration of objects in centripetal motions can be found with the following equation:

`a = \omega^(2)\, r`,

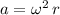Where:

• 
  `\omega` is the angular velocity of the object, and
• 
  `r` is the radius of the orbit.

Let
`m` denote the mass of this asteroid. Apply Newton's Laws of Motion to derive the net force on this asteroid:

`\displaystyle F_{\text{net}} = m\, a = m\, \omega^(2)\, r`.

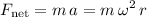The magnitude of the gravitational attraction between the Sun and this asteroid can be found with the following expression:

`\displaystyle (\text{gravitational attraction}) = (G\, M\, m)/(r^(2))`,

Where:

• 
  `G` is the gravitational constant,
• 
  `M` is the mass of the Sun,
• 
  `m` is the mass of this asteroid, and
• 
  `r` is the radius of the circular orbit.

Assume that the asteroid is not under the influence of gravity of any object other than the sun. The net force on the asteroid would be equal to the gravitational attraction from the Sun:

`\begin{aligned}& F_{\text{net}} \\ =\; & (\text{gravitational attraction}) \\ =\; & (G\, M\, m)/(r^(2))\end{aligned}`.

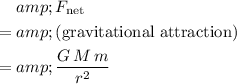Equate the two expressions for the net force on this asteroid and solve for the radius
`r` of the orbit:

`\displaystyle m\, \omega^(2)\, r = F_{\text{net}} = (G\, M\, m)/(r^(2))`.

`\displaystyle r^(3) = (G\, M\, m)/(m\, \omega^(2)) = (G\, M)/(\omega^(2))`.

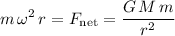`\displaystyle r = \left((G\, M)/(\omega^(2))\right)^(1/3) = \sqrt[3]{(G\, M)/(\omega^(2))}`.

Note that the expression for orbital radius
`r` does not include the mass
`m` of the asteroid. In other words, assuming that the orbital velocity and the mass of the Sun are both fixed, the orbital radius is independent from the mass of the asteroid.