Question

A carnival ferris wheel with a radius of 14 meters makes one complete revolution every 16 seconds. The bottom of the wheel is 1.5 meters above the ground if a person is at the top of the wheel when a stopwatch is started, determine how high above the ground that person will be after 2 minutes.

Equation for function: H(t)=_cos(_t)+_
Height after 2 minutes: _ meters


​

Answer 1

`H(t) = 14 \cos\left((\pi)/(8)t\right) + 15.5`

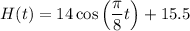
1.5 metres

Explanation:

The height of the person on the carnival ferris wheel can be modeled using a cosine function.

The general equation for a cosine function is:

`\large\boxed{H(t) = A \cos(B(t - C)) + D}`

where:

• |A| is the amplitude (half the vertical distance between the maximum and minimum values).
• 2π/B = period (horizontal length of one cycle of the curve).
• C = phase shift (horizontal shift - positive is to the left).
• D = vertical shift.

Given:

• Radius of the ferris wheel, r = 14 meters
• Period of one revolution = 16 seconds
• Initial height above the ground, h = 1.5 meters

In this case, the amplitude is half the difference between the highest and lowest points of the wheel's motion, i.e. the radius of the wheel. Therefore, the amplitude is A = 14.

As the period of one revolution is 16 seconds:

`(2\pi)/(B)=16 \implies B=(2\pi)/(16)\implies B=(\pi)/(8)`

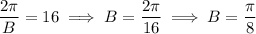
The parent cosine function crosses the y-axis at its maximum y = 1. Therefore, as we start timing when the person is at the top (maximum), the phase shift is C = 0.

The vertical shift is the sum of the radius (14 m) and the distance between the ground and the bottom of the wheel (1.5 m):

`D = 14+1.5=15.5`

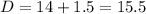
So, the equation for the height function H(t) is:

`\large\boxed{H(t) = 14 \cos\left((\pi)/(8)t\right) + 15.5}`

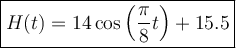
where t is time in seconds.

`\hrulefill`

To find the height after 2 minutes, first convert 2 minutes to seconds:

`\rm 2 \;minutes=2 * 60=120\;seconds`

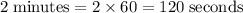
Substitute t = 120 into function H(t):

`\begin{aligned}{H(120)& = 14 \cos\left((\pi)/(8)\cdot 120\right) + 15.5\\\\& = 14 \cos\left(15\pi\right) + 15.5\\\\& = 14 (-1) + 15.5\\\\& = -14 + 15.5\\\\& = 1.5\end{aligned}`

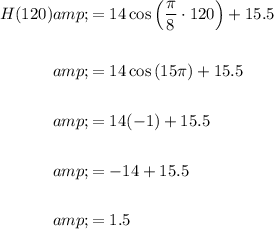
Therefore, the height of the person above the ground after 2 minutes is 1.5 meters.