Question

If f(g) = 2g + 2 and g(x) = -2x, what is f(g(x)) in terms of x?

Answer 1

`\boxed{-4x + 2}`

Explanation:

Given,

• f(g) = 2g + 2 (f is a function of g)
• g(x) = -2x (g is a function of x)

The composite result function, f(g(x)) = f(-2x). Evaluate f(-2x) by substituting the value of g into f,

`f( - 2x) = 2( - 2x) + 2`

Simplifying,

`f( - 2x) = - 4x + 2`

Hence, f(g(x)) in terms of x is -4x + 2.

Answer 2

Answer: f(g(x)) = -4x + 2

Explanation:

Our task is to evaluate the following function:
`\sf{f(g)(x))}`.

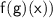This operation is known as composition of functions - we plug one function into another one.

When:

• f(x) = 2x + 2
• g(x) = -2x

Plug "g" into "f":

• f(x) = 2(-2x) + 2
• f(x) = -4x + 2

Our answer is f(g(x)) = -4x + 2 ^^"

Note that it's important to do it in the right order - if we have f(g(x)), we plug "g" into "f" and evaluate, not the other way around.