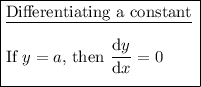Question

Find the derivative of the function. Simplify and express the answer using positive exponents only.

y = (x² - 8)(x + 1)

Answer 1

`\frac{\text{d}y}{\text{d}x}&=3x^2+2x-8`

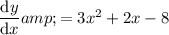
Explanation:

To find the derivative of the function y = (x² - 8)(x + 1), we can use the product rule.

`\boxed{\begin{array}{l}\underline{\sf Product\;Rule\;for\;Differentiation}\\\\\textsf{If}\;y=uv\;\textsf{then:}\\\\\frac{\text{d}y}{\text{d}x}=u\frac{\text{d}v}{\text{d}x}+v\frac{\text{d}u}{\text{d}x}\\\\\end{array}}`

`\textsf{Let}\;u = x^2 - 8`

`\textsf{Let}\;v = x+1`

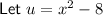
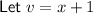
Differentiate u and v with respect to x:

`\frac{\text{d}u}{\text{d}x}=2 \cdot x^(2-1)-0=2x`

`\frac{\text{d}v}{\text{d}x}=x^(1-1)+0=x^0=1`

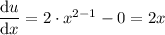
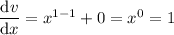
Substitute the expressions into the product rule formula:

`\frac{\text{d}y}{\text{d}x}&=u\frac{\text{d}v}{\text{d}x}+v\frac{\text{d}u}{\text{d}x}`

`\frac{\text{d}y}{\text{d}x}&=(x^2-8)\cdot 1+(x+1)\cdot 2x`

`\frac{\text{d}y}{\text{d}x}&=(x^2-8)+2x(x+1)`

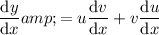
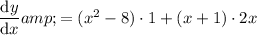
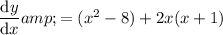
Simplify:

`\frac{\text{d}y}{\text{d}x}&=x^2-8+2x^2+2x`

`\frac{\text{d}y}{\text{d}x}&=3x^2+2x-8`

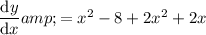
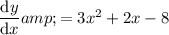
Therefore, the derivative of the given function is:

`\large\boxed{\frac{\text{d}y}{\text{d}x}&=3x^2+2x-8}`

`\hrulefill`

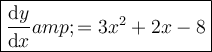
Differentiation Rules

`\boxed{\begin{minipage}{4.5 cm}\underline{Differentiating $x^n$}\\\\If $y=x^n$, then $\frac{\text{d}y}{\text{d}x}=nx^(n-1)$\\\end{minipage}}`

`\boxed{\begin{minipage}{4 cm}\underline{Differentiating $ax$}\\\\If $y=ax$, then $\frac{\text{d}y}{\text{d}x}=a$\\\end{minipage}}`

`\boxed{\begin{minipage}{4cm}\underline{Differentiating a constant}\\\\If $y=a$, then $\frac{\text{d}y}{\text{d}x}=0$\\\end{minipage}}`