Question

How long will it take $12,500 to increase to $16,000, if it is invested at 2.5% compounded continuously?

Answer 1

t = 9.88 (since units are not given we cannot write those, could be seconds, minutes or months etc)

Explanation:

For continuous compounding interest, we have the formula,

`P(t) = Ae^(rt)\\`

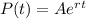
where P(t) is the value at time t

t is time

A is the original amount

r is the rate

In our case,

r = 2.5% = 0.025

A = 12,500

P(t) = 16,000

And we have to find t, so,

`P(t) = Ae^(rt)\\Solving \ for \ t,\\P(t)/A=e^(rt)\\taking \ ln \\ln(P(t)/A)=rt\\t = ln(P(t)/A)/r\\putting \ values,\\t = ln(16000/12500)/0.025\\t=ln(32/25)/0.025\\t = 0.247/0.025\\t=9.88`

t = 9.88 (since units are not given we cannot write those, could be seconds, minutes or months)