The function F is:
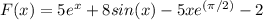
Given Information:
We start with a second-order linear differential equation:
![\[ f^(\prime\prime)(x) = 5e^x - 8\sin(x) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/cngp63d7mvgse7gzbni0ssrt8oep8g2cw2.png)
Along with the following initial conditions:
![\[ f(0) = 3, f\left((\pi)/(2)\right) = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/khcxd435127ezxnli2gso63vx97rvsnsf8.png)
Integration to Find
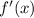 :
:
To find the first derivative
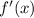 , we integrate the given second derivative:
, we integrate the given second derivative:
![\[ \int (5e^x - 8\sin(x)) \,dx = 5e^x + 8\cos(x) + C_1 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/hsv5fjfk4aky7fweddqz6v9zh39yzcy9ph.png)
Here,
 is the constant of integration.
is the constant of integration.
Application of Initial Condition for
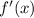 :
:
Using the initial condition
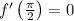 , we substitute
, we substitute
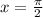 into the expression for
into the expression for
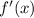 :
:
![\[ 5e^{(\pi)/(2)} + 8\cos\left((\pi)/(2)\right) + C_1 = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/crmsomqveaxibn90qks7fpm2fme79pjkd9.png)
Solving for
 , we get
, we get
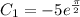 .
.
Integration to Find
 :
:
Integrating
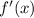 , we obtain
, we obtain
 :
:
![\[ \int (5e^x + 8\cos(x) - 5e^{(\pi)/(2)}) \,dx = 5e^x + 8\sin(x) - 5xe^{(\pi)/(2)} + C_2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/2ch59wikdlvjh9uyoygrgwr8blj0ki6mgd.png)
Here,
 is the constant of integration.
is the constant of integration.
Application of Initial Condition for
 :
:
Using the initial condition
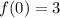 , we substitute
, we substitute
 into the expression for
into the expression for
 :
:
![\[ 5 + 8\sin(0) - 5(0)e^{(\pi)/(2)} + C_2 = 3 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/gn0081nl9dn2cilvvurebp3sofd5t3czm4.png)
Solving for
 , we get
, we get
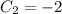
Final Solution:
Combining the expressions for
 and the determined constants, the solution to the differential equation with the given initial conditions is:
and the determined constants, the solution to the differential equation with the given initial conditions is:
![\[ f(x) = 5e^x + 8\sin(x) - 5xe^{(\pi)/(2)} - 2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/t0q7cn27q6r1dh4mlmx6a2ltxalw1wqymy.png)