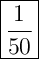Question

Need help full steps to solve…

Answer 1

`(2^(p+1)\cdot 3^(2p-q)\cdot 5^(p+q)\cdot 6^q)/(6^p \cdot 10^(q+2)\cdot 15^p)=\boxed{(1)/(50)}`

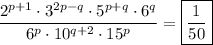
Explanation:

Given expression:

`(2^(p+1)\cdot 3^(2p-q)\cdot 5^(p+q)\cdot 6^q)/(6^p \cdot 10^(q+2)\cdot 15^p)`

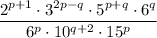
To simplify the given expression, use the laws of exponents to combine like terms and simplify.

`\boxed{\begin{array}{rl}\underline{\sf Laws\;of\;Exponents}\\\\\sf Product:&a^m * a^n=a^(m+n)\\\\\sf Quotient:&a^m / a^n=a^(m-n)\\\\\sf Power\;of\;a\;Power:&(a^m)^n=a^(mn)\\\\\sf Power\;of\;a\;Product:&(ab)^m=a^mb^m\\\\\sf Negative\;Exponent:&a^(-m)=(1)/(a^m)\\\\\sf Zero\;Exponent:&a^0=1\\\\\end{array}}`

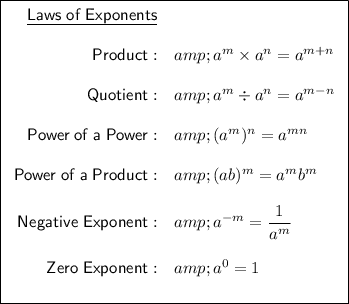
Use the product rule so that each base has one exponent:

`(2^(p)\cdot2^(1)\cdot 3^(2p)\cdot3^(-q)\cdot 5^(p)\cdot5^(q)\cdot 6^q)/(6^p \cdot 10^(q)\cdot10^(2)\cdot 15^p)`

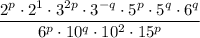
Apply the power of a power rule to simplify
`3^(2p)`:

`(2^(p)\cdot2^(1)\cdot (3^(2))^(p)\cdot3^(-q)\cdot 5^(p)\cdot5^(q)\cdot 6^q)/(6^p \cdot 10^(q)\cdot10^(2)\cdot 15^p)`

`(2^(p)\cdot2^(1)\cdot9^(p)\cdot3^(-q)\cdot 5^(p)\cdot5^(q)\cdot 6^q)/(6^p \cdot 10^(q)\cdot10^(2)\cdot 15^p)`

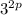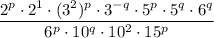
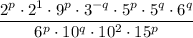
Rearrange to collect terms with the same exponent:

`(2^(1)\cdot2^(p)\cdot 5^(p)\cdot 9^(p)\cdot5^(q)\cdot 6^q\cdot3^(-q))/(10^(2)\cdot6^p\cdot 15^p \cdot 10^(q))`

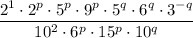
Apply the power of a product rule to simplify the terms with the same exponents:

`(2^(1)\cdot(2\cdot 5\cdot 9)^(p)\cdot(5\cdot 6)^q\cdot3^(-q))/(10^(2)\cdot(6\cdot 15)^p \cdot 10^(q))`

`(2^(1)\cdot90^(p)\cdot30^q\cdot3^(-q))/(10^(2)\cdot90^p \cdot 10^(q))`

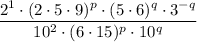
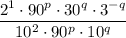
Cancel the common factor
`90^p`:

`(2^(1)\cdot30^q\cdot3^(-q))/(10^(2) \cdot 10^(q))`

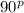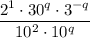
Apply the negative exponent rule to move
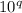`10^q` to the numerator:

`(2^(1)\cdot30^q\cdot3^(-q)\cdot 10^(-q))/(10^(2))`

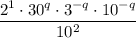
Use the power of a product rule to rewrite
`30^q`:

`(2^(1)\cdot(3 \cdot 10)^q\cdot3^(-q)\cdot 10^(-q))/(10^(2))`

`(2^(1)\cdot3^q \cdot 10^q\cdot3^(-q)\cdot 10^(-q))/(10^(2))`

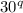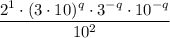
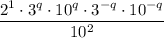
Rearrange to collect terms with the same base:

`(2^(1)\cdot3^q\cdot3^(-q) \cdot 10^q\cdot 10^(-q))/(10^(2))`

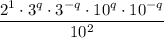
Apply the product rule to simplify the terms in the numerator:

`(2^(1)\cdot3^(q-q) \cdot 10^(q-q))/(10^(2))`

`(2^(1)\cdot3^(0) \cdot 10^(0))/(10^(2))`

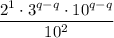
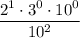
Apply the zero exponent rule, a⁰ = 1:

`(2^(1)\cdot1 \cdot 1)/(10^(2))`

`(2^(1))/(10^(2))`

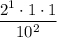
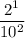
Simplify the powers of 2 and 10:

`(2)/(100)`

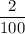
Divide the numerator and denominator by the highest common factor:

`(2/ 2)/(100/ 2)=(1)/(50)`

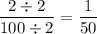
As the expression cannot be simplified further, the simplified expression is:

`\Large\boxed{(1)/(50)}`