Question

Question 8 A population of bacteria is growing according to the equation P(t)=950e^(0.03t). Estimate when the population will exceed 1043.

Answer 1

Answer: After 3; approximately 3.11314901 (time measurement)

Step-by-step explanation:

I dunno what the time measurement is.

To solve this problem, we have to understand the equation. The basic formula of this equation is
`A=Pe^(rt)`.

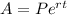In this equation:

A=Amount

P=Principal (Start amount)

e=2.71828

r=rate (growth/decay amount)

t=time (how long in years, days, weeks (etc.))

In our case, 950 is the start amount, 0.03 is the rate which in percentage is 3% and our targeted amount is higher than 1043.

Basically, that means we need to find after how much the time unit after the population is 1043 bacteria if we start out with 950 and it increases continuously by 3%.

Our new equation is
`1043=950e^(0.03t)`.

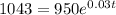Now we just need to solve it. It's easiest just to put this into a calculator, but to solve it normally, first divide the amount by the start amount
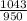`(1043)/(950)`. Our new equation is
`1.1=e^(0.03t)`.

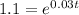Now we convert this to log form and get ln(1.1)=0.03t or
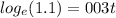`log_(e)(1.1)=003t`. ln(1.1) is about 0.1 and our equation is now 0.09=0.03t.

Finally we can divide
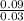`(0.09)/(0.03)` and we get 3.

But this is just the approximate estimation, the more specified answer is 3.11314901 time unit.

So after about 3 of the time unit, the bacteria population would exceed 1043.

Hope that helped a lot. Let me know any further questions.

:)