the couple can afford to borrow approximately $388,534 for their house with the given conditions.
To calculate the amount the couple can afford to borrow for a 30-year fixed-rate loan at 4.2% interest rate compounded monthly with a monthly house payment of $1,900, we use the formula for the present value of an annuity. Here's the step-by-step calculation:
1. Convert Annual Interest Rate to Monthly:
- Annual interest rate = 4.2% or 0.042 (as a decimal)
- Monthly interest rate = 0.042 / 12 = 0.0035 (or 0.35%)
2. Convert Loan Term to Months:
- Loan term = 30 years
- Loan term in months = 30 years * 12 months/year = 360 months
3. Use the Present Value of Annuity Formula:
- The formula is:
![\( P = PMT * \left[ (1 - (1 + r)^(-n))/(r) \right] \)](https://img.qammunity.org/2024/formulas/business/high-school/qedq04nxiugeoh7mzqxoto0cwkous3p4ig.png)
- Where
 is the loan amount,
is the loan amount,
 is the monthly payment,
is the monthly payment,
 is the monthly interest rate, and
is the monthly interest rate, and
 is the total number of payments (months)
is the total number of payments (months)
4. Plug in the Values:
-
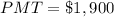
-
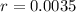
-
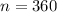
-
![\( P = 1900 * \left[ (1 - (1 + 0.0035)^(-360))/(0.0035) \right] \)](https://img.qammunity.org/2024/formulas/business/high-school/66rtyvhb67frnx1ama5s37w874aih9jkco.png)
5. Calculate and Round to the Nearest Dollar:
-
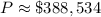 (rounded to the nearest dollar)
(rounded to the nearest dollar)
Therefore, the couple can afford to borrow approximately $388,534 for their house with the given conditions.