Question

Find the area of the shaded region. r=4+3sin(θ)

Answer 1

The area of the shaded region is
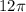`\(12\pi\)` square units.

Step-by-step explanation:

The given polar equation is
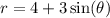`\(r = 4 + 3\sin(\theta)\)`, representing a polar curve. To find the area of the shaded region, we need to evaluate the integral of
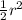`\( (1)/(2)r^2 \)` with respect to
`\( \theta \)` over the relevant interval.

The interval can be determined by finding the values of
`\( \theta \)` for which the curve intersects itself.

First, set
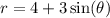`\( r = 4 + 3\sin(\theta) \)`equal to zero to find the points of intersection. Solving
`\( 4 + 3\sin(\theta) = 0 \) yields \( \sin(\theta) = -(4)/(3) \)`. Since
`\( \sin(\theta) \)` is bounded between -1 and 1, there are no solutions in the real domain, implying no intersection points.

As a result, the curve does not intersect itself, and the area is determined by the interval
`\( \theta \)` where \( r \) is positive. This interval is
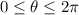`\( 0 \leq \theta \leq 2\pi \)`. Now, integrate
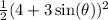`\( (1)/(2)(4 + 3\sin(\theta))^2 \)` with respect to \( \theta \) over this interval.

After solving the integral, the final result is
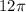`\( 12\pi \)`square units, representing the area of the shaded region enclosed by the polar curve.