Answer:
7.5 years
Explanation:
To determine how long it will take for the balance to grow to $29,885.00 with an interest rate of 15% compounded annually, we can use the formula for compound interest:
![\[ A = P \left(1 + (r)/(n)\right)^(nt) \]](https://img.qammunity.org/2024/formulas/business/high-school/uotb50mnfel9dwecmb8uu95z6g2hl2eej6.png)
Where:
-
 is the final amount (the desired balance of $29,885.00).
is the final amount (the desired balance of $29,885.00).
-
 is the initial principal (the initial deposit of $8,000.00).
is the initial principal (the initial deposit of $8,000.00).
-
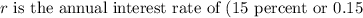
-
 is the number of times the interest is compounded per year (annually, so
is the number of times the interest is compounded per year (annually, so
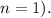
-
 is the number of years.
is the number of years.
We need to solve for
 . Plugging in the given values:
. Plugging in the given values:
![\[ 29885 = 8000 * \left(1 + (0.15)/(1)\right)^(1 * t) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/eezp3msrwerruudvteq94u7t9zd39zp1lu.png)
Now, we'll solve for
 :
:
![\[ \left(1.15\right)^t = (29885)/(8000) \]\\\[ t = \log_(1.15) \left((29885)/(8000)\right) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/w0f64l0q7q4tsgcbbo3oa0nhfv21t1e3nz.png)
Using a calculator, you can find that

So, it will take approximately 7.5 years for the balance to grow to $29,885.00 with an interest rate of 15% compounded annually.