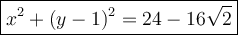Question

Write the equation of a circle whose center is O(0,1) and is tangent to the circle x² + y² - 4x - 6y = 3

Answer 1

`x^2+(y-1)^2=24-16√(2)`

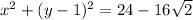
Explanation:

Two circles will touch as per the given diagram if the distance between their centres is equal to the difference between their radii.

`\boxed{\begin{minipage}{4 cm}\underline{Equation of a circle}\\\\$(x-h)^2+(y-k)^2=r^2$\\\\where:\\ \phantom{ww}$\bullet$ $(h, k)$ is the center. \\ \phantom{ww}$\bullet$ $r$ is the radius.\\\end{minipage}}`

Rewrite the given circle equation in standard form by completing the square:

`\begin{aligned}x^2+y^2-4x-6y&=3\\\\x^2-4x+y^2-6y&=3\\\\x^2-4x+\left((-4)/(2)\right)^2+y^2-6y+\left((-6)/(2)\right)^2&=3+\left((-4)/(2)\right)^2+\left((-6)/(2)\right)^2\\\\x^2-4x+4+y^2-6y+9&=3+4+9\\\\(x-2)^2+(y-3)^2&=16\end{aligned}`

Comparing this with the standard form, we get

• Center = (2, 3)
• r² = 16 ⇒ r = 4

We are told that the center of the smaller circle is (0, 1).

Therefore, we can find the distance between the centers of the two circles by using substituting the centers (0, 1) and (2, 3) into the distance formula:

`\begin{aligned}d&=√((x_2-x_1)^2+(y_2-y_1)^2)\\\\d&=√((2-0)^2+(3-1)^2)\\\\d&=√((2)^2+(2)^2)\\\\d&=√(4+4)\\\\d&=√(8)\\\\d&=√(2^2 \cdot 2)\\\\d&=√(2^2)√(2)\\\\d&=2√(2)\end{aligned}`

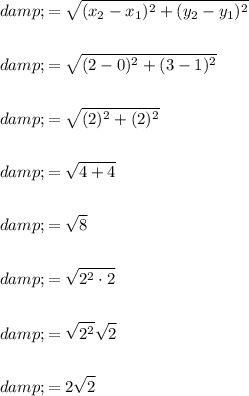
Therefore, the distance between the two centers is 2√2.

To determine the radius of the smaller circle, we can equate the distance between the centres of the two circles to the difference between their radii.

Let r₁ be the radius of the smaller circle with center (0, 1).

Let r₂ be the radius of the larger circle, so r₂ = 4.

Therefore:

`\begin{aligned}\textsf{Distance between centers}&=r_2-r_1\\2√(2)&=4-r_1\\r_1&=4-2√(2)\end{aligned}`

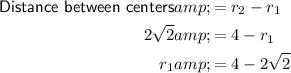
Therefore, the radius of the smaller circle is 4 - 2√2.

To write the equation of the smaller circle, substitute h = 0, k = 1 and r = 4 - 2√2 into the equation of a circle formula:

`\begin{aligned}(x-0)^2+(y-1)^2&=(4-2√(2))^2\\x^2+(y-1)^2&=24-16√(2)\end{aligned}`

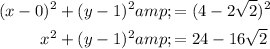
Therefore, the equation of the circle with center (0, 1) that is tangent to the circle x² + y² - 4x - 6y = 3 is:

`\large\boxed{x^2+(y-1)^2=24-16√(2)}`