Question

AP Calculus BC - Solving Integrals using Trig Identities and Other Methods:

I have two questions for this one. One of them, the first, I generally know how to do, but would be good if someone could show all steps and walk me through it.


For the second one, I have no clue how to do it. It would be nice if someone could show me all the steps and final solution.

Answer 1

`\text{1)}\quad\ln\left|(1)/(3)(x+√(x^2-9))\right|-(√(x^2-9))/(x)+C`

`\textsf{2)} \quad x+2\ln|x-1|-(1)/(x-1)+C`

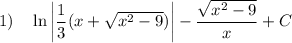
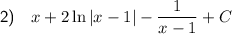
Explanation:

Question 1

Given integral:

`\displaystyle \int (√(x^2-9))/(x^2)\;dx`

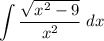
To solve the given integral, we can use trigonometric substitution.

`\boxed{\textsf{For\;$√(x^2-a^2)$ use the substitution $x=a\sec \theta$.}}`

The numerator of the rational function can be rewritten as
`√(x^2-3^2)`, so a = 3. Therefore:

`\textsf{Let}\;x=3\sec \theta`

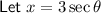
Start by differentiating u with respect to θ, and rearrange the equation to isolate dx:

`(dx)/(d\theta)=3\sec\theta\tan\theta\implies dx=3\sec\theta\tan\theta\;d\theta`

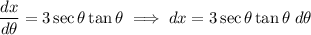
Rewrite the original integral in terms of θ and dθ:

`\begin{aligned}\displaystyle \int (√(x^2-9))/(x^2)\;dx&=\int (√((3\sec \theta)^2-9))/((3\sec \theta)^2)\cdot3\sec\theta\tan\theta\;d\theta\\\\&=\int (√(9\sec^2\theta-9))/(9\sec^2\theta)\cdot3\sec\theta\tan\theta\;d\theta\\\\&=\int (√(9(\sec^2\theta-1)))/(9\sec^2\theta)\cdot3\sec\theta\tan\theta\;d\theta\\\\&=\int(√(9\tan^2\theta))/(9\sec^2\theta)\cdot3\sec\theta\tan\theta\;d\theta\end{aligned}`

`\begin{aligned}&=\int(3\tan\theta)/(9\sec^2\theta)\cdot3\sec\theta\tan\theta\;d\theta\\\\&=\int(\tan^2\theta)/(\sec\theta)\;d\theta\\\\&=\int (\sin^2\theta)/(\cos^2\theta)\cdot \cos\theta\;d\theta\\\\&=\int(\sin^2\theta)/(\cos\theta)\;d\theta\\\\&=\int(1-\cos^2\theta)/(\cos\theta)\;d\theta\\\\&=\int(1)/(\cos \theta)-\cos\theta\;d\theta\\\\&=\int\sec\theta-\cos\theta\;d\theta\\\\&=\ln|\sec\theta+\tan\theta|-\sin\theta+C\end{aligned}`

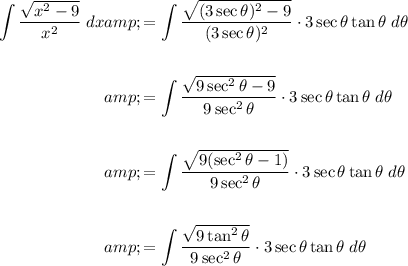
As x = 3secθ, then:

`\sec\theta=(x)/(3)\implies \cos \theta=(3)/(x)\implies \sin \theta=(√(x^2-9))/(x)\implies \tan\theta=(√(x^2-9))/(3)`

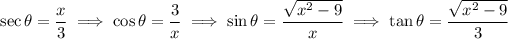
Substitute back in:

`=\ln\left|(x)/(3)+(√(x^2-9))/(3)\right|-(√(x^2-9))/(x)+C`

`=\ln\left|(1)/(3)(x+√(x^2-9))\right|-(√(x^2-9))/(x)+C`

`\hrulefill`

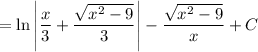
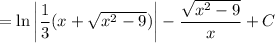
Question 2

Given integral:

`\displaystyle\int\left((x)/(x-1)\right)^2\;dx`

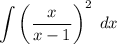
Use the substitution u = x - 1. Therefore, x = u + 1.

Differentiate u with respect to x, then isolate dx:

`(du)/(dx)=1\implies dx=du`

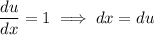
Rewrite the original integral in terms of u and du:

`\displaystyle\int\left((u+1)/(u)\right)^2\;du`

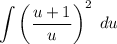
Simplify:

`\begin{aligned}\displaystyle\int\left((u+1)/(u)\right)^2\;du&=\int((u+1)^2)/(u^2)\;du\\\\&=\int(u^2+2u+1)/(u^2)\;du\\\\&=\int(u^2)/(u^2)+(2u)/(u^2)+(1)/(u^2)\;du\\\\&=\int 1\;du+2\int (1)/(u)\;du+\int u^(-2)\;du\end{aligned}`

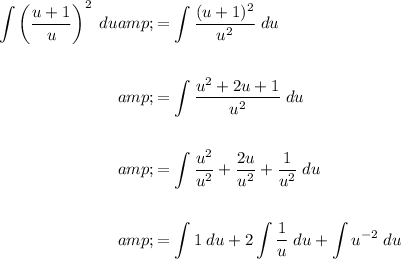
Evaluate each integral:

`\begin{aligned}&=u+2\ln|u|+(u^(-2+1))/(-2+1)+C\\\\&=u+2\ln|u|+(u^(-1))/(-1)+C\\\\&=u+2\ln|u|-(1)/(u)+C\end{aligned}`

Replace u with the original substitution:

`\begin{aligned}&=(x-1)+2\ln|x-1|-(1)/(x-1)+C\\\\&=x+2\ln|x-1|-(1)/(x-1)+C\end{aligned}`

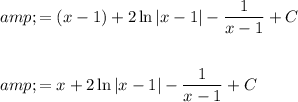
Note that we only need one constant of integration for the whole expression, so we can combine the constant -1 and C to be just C.

`\hrulefill`

`\boxed{\begin{array}{l}\underline{\textsf{Differentiation}}\\\\(d)/(dx)\sec(kx)=k\sec(kx)\tan(kx)\\\\(d)/(dx)ax=a\\\\\end{array}}`.

`\boxed{\begin{array}{l}\underline{\textsf{Integration\;(+\;constant)}}\\\\\displaystyle\int\sec(kx)\;dx=(1)/(k)\ln|\sec(kx)+\tan(kx)|\\\\\displaystyle\int \cos x\;dx=\sin x\\\\\displaystyle\int a \;dx=ax\\\\\displaystyle\int (1)/(x)\;dx=\ln|x|\\\\\displaystyle\int x^n\;dx=(x^(n+1))/(n+1)\\\\\end{array}}`