Answer:
AB = 5√(13) m ≈ 18.028 m (3 d.p.)
Total distance = 46,056 mm (nearest millimeter)
Explanation:
From observation of the given diagram, we can see that AB and CD are the hypotenuse of two right triangles. Therefore, to calculate the lengths of AB and CD, we can use Pythagoras Theorem.

For AB, the height of the right triangle is 10 m, and the base is the difference of 30 m and 15 m. Therefore:
Substitute the values of a, b and c into the formula and solve for AB:
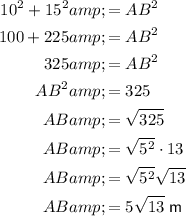
For CD, the height of the right triangle is 10 m, and the base is the difference of 50 m and 35 m. Therefore:
As the values of a and b are the same as those for the calculation of length AB, this means that CD = AB:
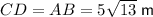
To calculate the total distance, sum the distances from A to E:
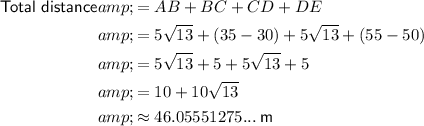
As there are 1000 millimeters in one meter, to convert meters to millimeters, multiply the number of meters by 1000:

Therefore, the total distance walked/climbed from the stage to the end of the walkway is 46,056 mm, rounded to the nearest millimeter.