Question

a sport car is advertised to have a maximum cornering acceleration of 0.85 g. what is its maximum speed for a 50-m radius curve? show all necessary steps.

Answer 1

Approximately
`20\; {\rm m\cdot s^(-1)}` (rounded to two significant figures, assuming that
`g = 9.81\; {\rm m\cdot s^(-2)}`.)

Step-by-step explanation:

When an object travels along a circular path, the centripetal acceleration of that object would be:

`\displaystyle a = (v^(2))/(r)`,

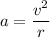Where:

• 
  `v` is the linear speed, and
• 
  `r` is the radius of the circular path.

Thus, the acceleration of this vehicle would be proportional to the square of its velocity. As linear velocity increases, the acceleration required would also increase.

Given the upper limit on the acceleration of the vehicle, the maximum possible velocity can be found with the following steps:

• Rearrange the equation
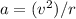  `a = (v^(2)) / r` to find an expression for linear velocity
  `v` in terms of acceleration
  `a` and radius
  `r`.
• Set the acceleration of the vehicle to the maximum possible value. Evaluate the expression from the previous step to find the value of velocity
  `v`.

Rearrange the equation for centripetal acceleration to find an expression for the linear velocity of the vehicle:

`\begin{aligned}v^(2) = a\, r\end{aligned}`.

`\begin{aligned}v = √(a\, r)\end{aligned}`.

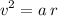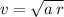It is given that the radius of this curve is
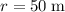`r = 50\; {\rm m}`. Substitute in the maximum possible value of acceleration
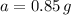`a = 0.85\, g` (assuming that
`g = 9.81\; {\rm m\cdot s^(-2)}`) to find the value of velocity:

`\begin{aligned}v &= √(a\, r) \\ &= √((0.85\, (9.81))\, (50))\; {\rm m\cdot s^(-1)} \\ &\approx 20\; {\rm m\cdot s^(-1)}\end{aligned}`.

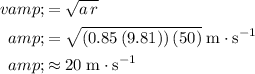(Rounded to two significant figures.)