Question

Tan^2(Q/2) - 2tan(Q/2) - 3 = 0

Answer 1

Great question! It seems like you have a quadratic equation involving the tangent function. To solve this equation, we can use a substitution to simplify it.

Let's make the substitution u = tan(Q/2). By doing this, we can rewrite the equation as u^2 - 2u - 3 = 0. Now we have a quadratic equation in terms of u.

To solve this quadratic equation, we can factor it or use the quadratic formula. Factoring the equation, we have (u - 3)(u + 1) = 0.

Setting each factor equal to zero, we get u - 3 = 0 or u + 1 = 0. Solving these equations, we find u = 3 or u = -1.

However, we need to remember that u = tan(Q/2). So, tan(Q/2) = 3 or tan(Q/2) = -1.

To find Q, we can use the inverse tangent function (also known as arctan or tan^(-1)). Taking the inverse tangent of both sides, we have Q/2 = arctan(3) or Q/2 = arctan(-1).

Now, we can solve for Q by multiplying both sides by 2: Q = 2 arctan(3) or Q = 2 arctan(-1).

Remember to check the domain and range of the inverse tangent function to ensure that the solutions are within the appropriate range.

I hope this helps! Let me know if you have any further questions.

Answer 2

`\sf Q = 142.13^\circ + 360^\circ k`

`\sf Q = -90^\circ + 360^\circ k`

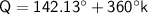
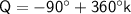
Explanation:

In order to solve the quadratic equation:

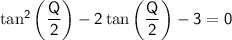`\sf \tan^2\left((Q)/(2)\right) - 2\tan\left((Q)/(2)\right) - 3 = 0` for Q.

we can use a substitution to simplify the equation.

Let's define:

`\sf x = \tan\left((Q)/(2)\right)`

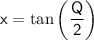
So, the equation becomes:

`\sf x^2 - 2x - 3 = 0`

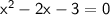
This is a quadratic equation in terms of x.

To solve for x, we can use the quadratic formula:

`\sf x = (-b \pm √(b^2 - 4ac))/(2a)`

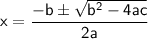
In this case, the coefficients are a = 1, b = -2, and c = -3.

Substituting these values into the quadratic formula:

`\sf x = (-(-2) \pm √((-2)^2 - 4 \cdot 1 \cdot (-3)))/(2 \cdot 1)`

`\sf x = (2 \pm √(4 + 12))/(2)`

`\sf x = (2 \pm √(16))/(2)`

`\sf x = (2 \pm 4)/(2)`

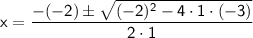
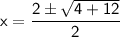
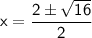
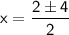
So, we have two possible solutions for x.

`\sf x = (2 + 4)/(2) = 3`

`\sf x = (2 - 4)/(2) = -1`

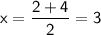
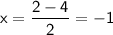
Now, we'll use the relationship
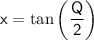`\sf x = \tan\left((Q)/(2)\right)` to find the corresponding values of Q.

For
`\sf x = 3`:

`\sf \tan\left((Q)/(2)\right) = 3`

`\sf (Q)/(2) = \arctan(3)`

`\sf Q = 2 \cdot \arctan(3)`

`\sf Q = 2 \cdot 71.565^\circ`

`\sf Q = 142.13^\circ`

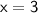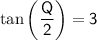
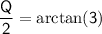
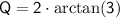
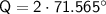
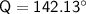
For
`\sf x = -1`:

`\sf \tan\left((Q)/(2)\right) = -1`

`\sf (Q)/(2) = \arctan(-1)`

`\sf Q = 2 \cdot \arctan(-1)`

`\sf Q = 2 \cdot -45^\circ`

`\sf Q =-90^\circ`

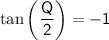
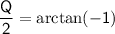
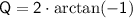
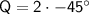
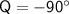
Keep in mind that the arctangent function has multiple angles that satisfy its equation.

So, the solutions for Q can also be represented as:

`\sf Q = 142.13^\circ + 360^\circ k`

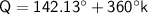
and

`\sf Q = -90^\circ + 360^\circ k`

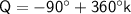
where K is an integer allowing for multiple solutions due to the periodic nature of the tangent function.