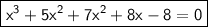3=5x^2+8x+x^3+7x^2-5 write expression in standard form

Question

asked Apr 14, 2024 154k views

1 Answer

Ansgar Wiechers · Answer 1 · 2024-04-20T16:51:59+0000

Answer:

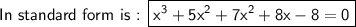
$\textsf{In standard form is : } \boxed{\sf x^3 + 5x^2 + 7x^2 + 8x -8 =0}$

Explanation:

Standard Form:

In mathematics, standard form refers to the most common way to write a mathematical expression, equation, or number.

For quadratic equations, the standard form is typically written as:

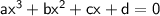
$\sf ax^3 + bx^2 + cx + d = 0$

Where a, b, c, and d are constants, and a is not equal to 0.

Expression in Standard Form:

Given the expression:

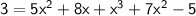
$\sf 3 = 5x^2 + 8x + x^3 + 7x^2 - 5$

Let's arrange the terms in descending order of the degree of x, and combine like terms to rewrite it in standard form:

Rearrange the terms:

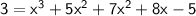
$\sf 3 = x^3 + 5x^2 + 7x^2 + 8x -5$

Combine like terms:

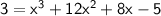
$\sf 3 = x^3 + 12x^2 + 8x -5$

Subtract 3 on both sides.

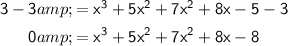
$\sf \begin{aligned} \sf 3 -3 &= \sf x^3 + 5x^2 + 7x^2 + 8x -5-3\\\sf 0 &=\sf x^3 + 5x^2 + 7x^2 + 8x -8 \end{aligned}$

Now, the expression in standard form for a cubic equation is:

$\boxed{\sf x^3 + 5x^2 + 7x^2 + 8x -8 =0}$