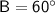Question

Instructions: Use trigonometry to find the unknown parts of the right triangle. A right triangle, ABC with, with sides, a, b, and hypotenuse c has one angle A=pi/6 and c = 20. Find the unknown sides and angle of the triangle.

a=10

b= ?

B= ? degrees​

Answer 1

`\sf b=10√(3)`

`\sf B =60^\circ`

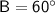
Explanation:

Given:

• Triangle ABC is a right triangle
• Angle A = pi/6 = 30 degrees
• c = 20
• a = 10

To find:

• b
• Angle B

Note:

Using trigonometric ratios, we can relate the sides and angles of a right triangle:

`\textsf{ Sine Ratio: sin(A) =}\sf ( opposite )/(hypotenuse)`

`\textsf{Cosine Ratio: cos(A) =}\sf ( adjacent )/( hypotenuse)`

`\textsf{Tangent Ratio: tan(A) =}\sf ( opposite )/( adjacent)`

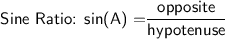
Calculations:

In right angled triangle with respect to A.

• Opposite = a = 10
• Adjacent = b
• Hypotenuse = c = 20

Side b:

We know that the cosine of angle A is equal to the adjacent side divided by the hypotenuse. We can use the sine formula to write this as:

`\sf cos\left(( 180^\circ )/(6)\right) =(Adjacent)/(Hypotenuse)=(b)/(c)`

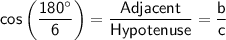
Note:
`\sf here\: \boxed{\sf \pi = 180^\circ}`

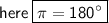
Substituting value

`\sf cos 30^\circ = (b)/(20)`

`\sf (√(3))/(2) = (b)/(30)`

`\textsf{Since value of }\sf cos30^\circ =(√(3))/(2)`

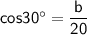
Doing criss cross multiplication:

`\sf (√(3))/(2) * 20= b`

`\sf b=10√(3)`

`\dotfill`

Angle B:

In right angled triangle with respect to B.

• 
  `\sf Opposite =\sf b=10√(3)`
• Adjacent = a = 10
• Hypotenuse = c = 20

We know that the cosine of angle B is equal to the adjacent side divided by the hypotenuse.

We can use the cosine formula to write this as:

`\sf cos(B)=(Adjacent)/(Hypotenuse)=(a)/(c)`

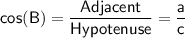
Substituting value

`\sf cos (B) =(10)/(20)`

`\sf cos (B) =(1)/(2)`

`\sf B = cos^(-1)\left((1)/(2)\right)`

`\sf B =60^\circ`

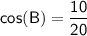
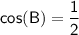
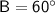
In terms of π.

`\sf B = (60^\circ * \pi)/(180^\circ)`

`\sf B = (\pi)/(3)`

`\dotfill`

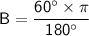
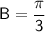
Summary:

`\sf b=10√(3)`

`\sf B =60^\circ`