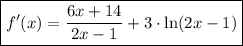Answer:
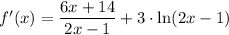
Explanation:
We can find the derivative of (the slope of the tangent line to) the function:
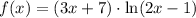
using the following rules:
- the product rule ...
![\left[\frac{}{} f(x) \cdot g(x) \frac{}{}\right]' = f(x) \cdot g'(x) + g(x)\cdot f'(x)](https://img.qammunity.org/2024/formulas/mathematics/high-school/u8lnm6guyassgoc1sqiygmrbbl2mlwyqvx.png)
- the chain rule ...
![\left[\frac{}{}f(g(x)\frac{}{}\right]' = f'\left(\frac{}{}g(x)\frac{}{}\right) \cdot g'(x)](https://img.qammunity.org/2024/formulas/mathematics/high-school/qqq46zsvre6mpt336vt1sl7eju5flds4es.png)
First, we can apply the product rule, identifying the factors (functions) as:
- 1st:

- 2nd:

We can find their derivatives by identifying the slope of the first factor and applying the chain rule to the second factor, where the function composition is
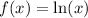 and
and
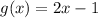 .
.
- 1st:
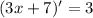
- 2nd:
![\left[\frac{}{}\ln(2x-1)\frac{}{} \right]' = (2)/(2x-1)](https://img.qammunity.org/2024/formulas/mathematics/high-school/qwxymbx0x7fi2khqwbdbfbxseqyikpvni2.png)
Next, we plug these values into the product rule to construct an unsimplified form of the derivative.
![f'(x) = (3x+7)\left[(2)/(2x-1)\right] + \ln(2x-1)\left[\frac{}{}3\frac{}{}\right]](https://img.qammunity.org/2024/formulas/mathematics/high-school/mic67tdyjpcmakyc03nnikqu7bmcdwphei.png)
Finally, this can be simplified by executing the possible instances of multiplication.