Determine whether f(x)=(x^(2)-3x)/(x^(2)-x-6) is continuous at x=3. If discontinuous, identify the type of discontinuity as infinite, jump, or removable.

Question

asked Jun 25, 2024 222k views

1 Answer

Philomath · Answer 1 · 2024-07-01T19:00:58+0000

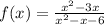
$f(x) = \frac{ { {x}^(2) - 3x } }{x {}^(2) - x - 6 } \\$

We want to study the continuity of the function around x=3 , so we have to take the limit:

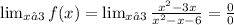
$\lim_(x→3)f(x) = \lim_(x→3)\frac{ { {x}^(2) - 3x } }{x {}^(2) - x - 6 } = (0)/(0 ) \\$

The limit is of the form 0/0 , so we can either apply L'Hopital's Rule for indeterminate limits or we can factor out the terms:

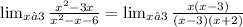
$\lim_(x→3)\frac{ { {x}^(2) - 3x } }{x {}^(2) - x - 6 } = \lim_(x→3)\frac{ { x(x - 3) } }{(x - 3)(x + 2) } \\$

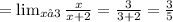
$= \lim_(x→3)\frac{ { x } }{x + 2} = (3)/(3 + 2) = (3)/(5) \\$

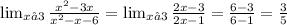
$\lim_(x→3)\frac{ { {x}^(2) - 3x } }{x {}^(2) - x - 6 } = \lim_(x→3)( 2x - 3 )/(2x - 1 ) = (6 - 3)/(6 - 1) = (3)/(5) \\$

(differentiate the numerator and denominator)

The limit as x approaches 3 is equal to 3/5 , thus the function admits a hole/point discontinuity at the point of coordinates (3 ; 3/5)