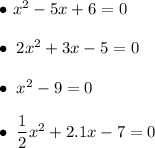Question

Could someone give me an example of an quadratic equation

Answer 1

Refer to the step-by-step explanation. A list of examples is at the very bottom of the explanation.

Explanation:
`\hrulefill`

What is a quadratic equation?
`\hrulefill`

A quadratic equation is a type of polynomial equation of the second degree, which means it contains terms with variables raised to the power of 2. In general, a quadratic equation has the form:

`\boxed{\left\begin{array}{ccc}\text{\underline{A Quadratic Equation:}}\\\\ax^2+bx+c=0\\\\\text{Where:}\\\bullet \ a, \ b, \ \text{and} \ c \ \text{are }\bold{constants}\\ \bullet \ a\\eq 0\end{array}\right}`

Quadratic equations can have different forms and can involve real or complex numbers. The solutions to a quadratic equation can be real or complex numbers as well, depending on the discriminant in the quadratic formula. The discriminant helps determine whether the solutions are real or complex, and whether they are distinct or repeated. The discriminant (Δ) is calculated as:

`\boxed{\left\begin{array}{ccc}\text{\underline{The Discriminant:}}\\\\ \Delta=b^2-4ac\\\\\text{Where:}\\\bullet \ a, \ b, \ \text{and} \ c \ \text{are the} \ \bold{coefficients} \ \text{from the} \ \bold{quadratic \ equation}\\\\\\ \bullet \ \text{if} \ \Delta > 0, \text{then there are two real solutions of} \ x\\\bullet \ \text{if} \ \Delta = 0, \text{then there is one real solution for} \ x \ \\\bullet \ \text{if} \ \Delta < 0, \text{then there are two complex solutions for} \ x\end{array}\right}`

The discriminant is a valuable tool for understanding the behavior of quadratic equations and their solutions without actually solving the equation. It helps determine whether the solutions are real or complex and whether they are distinct or repeated. This information is particularly useful when graphing quadratic functions or when dealing with real-world problems that involve quadratic equations.

`\hrulefill`

How do we solve quadratic equations?
`\hrulefill`

Quadratic equations can be solved using various methods, but one of the most common and fundamental approaches is by using the quadratic formula. The quadratic formula provides a general method for finding the solutions of any quadratic equation of the form ax² + bx + c = 0. Here's the quadratic formula:

`\boxed{\left\begin{array}{ccc}\text{\underline{The Quadratic Formula:}}\\\\x=(-b\pm√(b^2-4ac) )/(2a) \\\\\text{Where:}\\\bullet \ a, \ b, \ \text{and} \ c \ \text{are the} \ \bold{coefficients} \ \text{from the} \ \bold{quadratic \ equation}\end{array}\right}`

It's important to note that the quadratic formula works for all quadratic equations, whether the coefficients are integers, fractions, decimals, or even complex numbers.

There are other methods to solve quadratic equations, each with its own advantages and use cases. Here's a list of other common methods:

• Factoring
• Completing the square
• Graphing

If you have any questions about the above methods, feel free to leave a question in the comments.

`\hrulefill`

Some example of a quadratic equation:
`\hrulefill`

Recall that the form of a quadratic equation is ax² + bx + c = 0, where a, b, and c are coefficients. We can make up any quadratic equation by changing these values, as long as a ≠ 0.

Here is a list of quadratic equations:

`\bullet \ x^2-5x+6=0\\\\\bullet \ 2x^2+3x-5=0\\\\\bullet \ x^2-9=0\\\\\bullet \ (1)/(2)x^2+2.1x-7=0`