Question

If the diameter of a circle is tripled, how does the area of the circle change?​

Answer 1

Explanation:

If the diameter of a circle is tripled, the new diameter becomes three times the original diameter. The relationship between the diameter (\(d\)) and the radius (\(r\)) of a circle is \(d = 2r\).

If the original diameter is \(d\) and the new diameter is \(3d\), then the original radius is \(r\) and the new radius is

large
`\(1.5r\).`

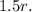
The formula for the area (\(A\)) of a circle is \(A = \pi r^2\).

If we compare the original area (\(A_1\)) with the new area (\(A_2\)):

\(A_1 = \pi r^2\) and \(A_2 = \pi (1.5r)^2\).

Simplifying the expression for \(A_2\), we get \(A_2 = \pi \cdot 2.25r^2\), which is 2.25 times the original area.

So, when the diameter of a circle is tripled, the area of the circle becomes 2.25 times larger.

Answer 2

Answer: The area has been multiplied by 9

=================================================

Explanation

Let's say we start with diameter = 2

That splits in half to a radius of 1

area = pi*(radius)^2

area = pi*1^2

area = pi

The number pi is approximately 3.14

Now we'll triple the diameter. We go from 2 to 2*3 = 6

A diameter of 6 leads to a radius of 3 (because 6/2 = 3)

Compute the new area

area = pi*(radius)^2

area = pi*3^2

area = 9pi

-------------

In summary

• old area = pi
• new area = 9pi

The area has been multiplied by 9