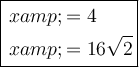Question

Solve the equation, logx 8 + log8 x = 13/6​

Answer 1

`x=4`

`x=16√(2)`

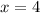
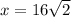
Explanation:

Given logarithmic equation:

`\log_x8+\log_8x=(13)/(6)`

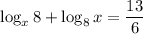
Use the change of base log rule to rewrite logₓ8 with a base of 8.

`\boxed{\begin{array}{l}\underline{\sf Change\;of\;base}\\\\\log_ba=(\log_xa)/(\log_xb)\end{array}}`

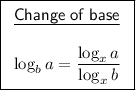
Therefore:

`\log_x8=(\log_88)/(\log_8x)`

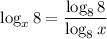
As logₐa = 1, then:

`\log_x8=(\log_88)/(\log_8x)=(1)/(\log_8x)`

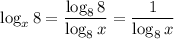
Substitute this into the original equation:

`(1)/(\log_8x)+\log_8x=(13)/(6)`

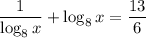
Rewrite the equation using u = log₈x:

`(1)/(u)+u=(13)/(6)`

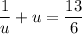
Rearrange the equation into a quadratic:

`(1)/(u)+u\cdot (u)/(u)=(13)/(6)`

`(1)/(u)+(u^2)/(u)=(13)/(6)`

`(1+u^2)/(u)=(13)/(6)`

`6(1+u^2)=13u`

`6u^2+6=13u`

`6u^2-13u+6=0`

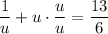
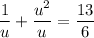
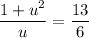
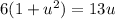
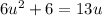
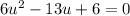
Solve for u using the quadratic formula.

`\boxed{\begin{array}{c}\underline{\sf Quadratic \;Formula}\\\\x=(-b \pm √(b^2-4ac))/(2a)\\\\\textsf{when}\; ax^2+bx+c=0 \\\end{array}}`

In this case, the coefficients are:

• 
  `a = 6`
• 
  `b=-13`
• 
  `c=6`

Substitute the coefficients into the quadratic formula, and solve for u:

`u=(-(-13) \pm √((-13)^2-4(6)(6)))/(2(6))`

`u=(13 \pm √(169-144))/(12)`

`u=(13 \pm √(25))/(12)`

`u=(13 \pm 5)/(12)`

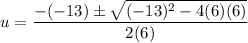
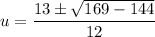
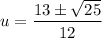
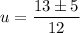
Therefore, the two values of u are:

`u=(13-5)/(12)=(8)/(12)=\boxed{(2)/(3)}`

`u=(13+5)/(12)=(18)/(12)=\boxed{(3)/(2)}`

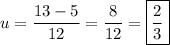
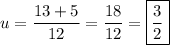
Substitute back u = log₈x:

`\log_8x=(2)/(3)`

`\log_8x=(3)/(2)`

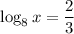
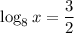
Solve for x using the log rule:

`\boxed{\log_ab=c \iff b=a^c}`

Therefore, the first value of x is:

`\begin{aligned}x&=8^{(2)/(3)}\\x&=(2^3)^{(2)/(3)}\\x&=2^{\left(3 \cdot (2)/(3)\right)}\\x&=2^2\\x&=4\end{aligned}`

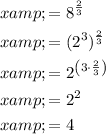
The second value of x is:

`\begin{aligned}x&=8^{(3)/(2)}\\x&=√(8^3)\\x&=√(512)\\x&=√(16^2\cdot2)\\x&=√(16^2)√(2)\\x&=16√(2)\end{aligned}`

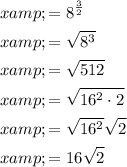
Therefore, the solutions to the given logarithmic equation are:

`\large\boxed{\begin{aligned}x&=4\\x&=16√(2)\end{aligned}}`