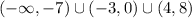Answer:
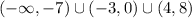
=============================================
Step-by-step explanation:
Recall that y = f(x)
Asking when f(x) < 0 is the same as y < 0.
We focus on the portions of the curve below the x axis where y is negative.
The interval to the left of x = -7 is the first such portion below the x axis.
This gives
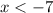 aka
aka
 and that condenses to the interval notation of
and that condenses to the interval notation of
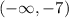 . We use a curved parenthesis to exclude x = -7. This is because x = -7 is a root and means y = f(-7) = 0.
. We use a curved parenthesis to exclude x = -7. This is because x = -7 is a root and means y = f(-7) = 0.
The next interval below the x axis is when
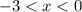 which condenses to the interval notation
which condenses to the interval notation

The last portion below the x axis is when
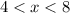 which condenses to the interval notation
which condenses to the interval notation

--------
In summary we found these three separate regions below the x axis
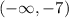 and
and
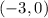 and
and

Each refers to interval notation.
Glue the regions together with the union symbol and we arrive at the final answer