Answer:
(a) Approximately
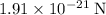 .
.
(b)
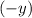 -direction.
-direction.
(c) Approximately
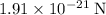 .
.
(d)
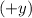 -direction.
-direction.
Step-by-step explanation:
The magnetic force on a moving charge can be found with the equation:
 ,
,
Where:
 is the electrostatic charge on the moving object (
is the electrostatic charge on the moving object (
 might be negative, as in the case of the electron,)
might be negative, as in the case of the electron,)
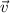 is the velocity vector of the moving object, and
is the velocity vector of the moving object, and
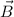 is the magnetic field vector.
is the magnetic field vector.
In this expression,
 is the vector cross-product between
is the vector cross-product between
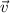 and
and
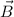 . Note the order of this cross-product: the velocity vector comes before the magnetic field vector.
. Note the order of this cross-product: the velocity vector comes before the magnetic field vector.
The electrostatic charge on a proton is equal to the elementary charge, a physical constant:
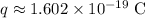 .
.
In this question, it is given that the speed (a scalar) of the proton is
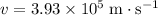 . Since this proton is moving in the positive
. Since this proton is moving in the positive
 -direction, the
-direction, the
 -component (first component) of the velocity vector
-component (first component) of the velocity vector
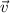 should be positive, while the other two components should be zero. Hence, the velocity vector of this proton would be:
should be positive, while the other two components should be zero. Hence, the velocity vector of this proton would be:
 .
.
Similarly, since the magnetic field points in the positive
 -direction, the
-direction, the
 -component of the magnetic field vector
-component of the magnetic field vector
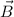 should be positive, while the other two components should be zero:
should be positive, while the other two components should be zero:
 .
.
The magnetic force on this proton would be:
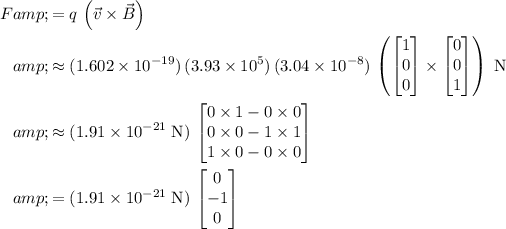 .
.
In other words, magnitude of the magnetic force on this proton would be approximately
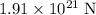 . Since the
. Since the
 -component of this force is negative while the
-component of this force is negative while the
 - and
- and
 -components are zero, this force would point in the
-components are zero, this force would point in the
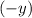 -direction (negative
-direction (negative
 direction.)
direction.)
The electrostatic charge on an electron is the opposite of that on a proton:
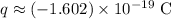 .
.
The value of
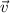 and
and
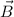 are the same as the ones in the case of the proton. The magnetic force vector on this electron would be:
are the same as the ones in the case of the proton. The magnetic force vector on this electron would be:
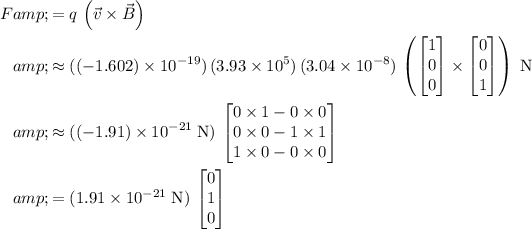 .
.
The magnitude of the magnetic force on the electron would be
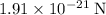 , same as that on the proton. While the
, same as that on the proton. While the
 - and
- and
 -components are still zero, this force vector would point in the
-components are still zero, this force vector would point in the
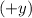 -direction (positive
-direction (positive
 -direction) since the
-direction) since the
 -component is now positive.
-component is now positive.