Question

A man wants to measure the height of a nearby tower. He places a 5 ft pole in the shadow of the tower so that the shadow of the pole is exactly covered by the shadow of the tower. The total length of the tower's shadow is 161 ft, and the pole casts a shadow that is 3.25 ft long. How tall is the tower? Round your answer to the nearest foot. (The figure is not drawn to scale.) Shadow of pol Pole Shadow of tower Sun Tower O X C​

Answer 1

~247.6923 ft

Explanation:

Since the man placed the pole in a position where the shadow of the tower exactly covers the shadow of the pole, it suggests that the triangles created with the shadow of the tower and the shadow of the pole are the same in shape, but not in size.

Thus, you can create a ratio between the length of the pole and the length of the shadow it produces and set it equivalent to the ratio between the height of the tower and the length of the shadow it produces since both triangles produce the same shape.

`(x)/(161) = (5)/(3.25)`

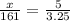
Next, simplify by multiplying 161 on both sides.

`x = (5)/(3.25) (161)`

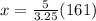
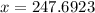`x = 247.6923` (approximately)